1 Exercices : chapitre vecteurs

Nom / Prénom : ...

Correction à partir des réponses de Gabrielle.

1.1 p 146 n° 89

1. trois paires de vecteurs égaux.

   • \(\overrightarrow{GE} = \overrightarrow{DC}\)
   • \(\overrightarrow{DE} = \overrightarrow{BA}\)
   • \(\overrightarrow{FB} = \overrightarrow{GD}\)

2. trois vecteurs de même direction.

   • \(\overrightarrow{EG}\)
   • \(\overrightarrow{CD}\)
   • \(\overrightarrow{AF}\)

3. quatre vecteurs de même norme.

   • \(\overrightarrow{BD}\)
   • \(\overrightarrow{FG}\)
   • \(\overrightarrow{FB}\)
   • \(\overrightarrow{GD}\)

4. deux vecteurs de même direction, de sens contraire et de normes différentes.

   • \(\overrightarrow{FE}\)
   • \(\overrightarrow{CA}\)

5. quatre vecteurs opposés au vecteur \(\overrightarrow{ED}\)

   • \(\overrightarrow{DE}\)
   • \(\overrightarrow{EF}\)
   • \(\overrightarrow{CB}\)
   • \(\overrightarrow{BA}\)

1.2 p 147 n° 96

Figure de l'énoncé, mais les questions de la partie 1 sont différentes. Dans cet exercice il faut utiliser la relation de Chasles et parfois remplacer un vecteur par un veteur égal, mais dont les extrémités permettent d'appliquer la relation de Chasles.

1. Réponse de la question a) : \(\overrightarrow{AB} + \overrightarrow{FA} = \overrightarrow{FA} + \overrightarrow{AB}\) car on peut changer l'ordre des termes dans la somme.

   \(\overrightarrow{FA} + \overrightarrow{AB} = \overrightarrow{FB}\) utilisation de la relation de Chasles.

   2. \(\overrightarrow{FD} + \overrightarrow{EB} = \overrightarrow{FD} + \overrightarrow{D...} = \overrightarrow{...}\)

   \(\overrightarrow{FD} + \overrightarrow{EB} = \overrightarrow{FD} + \overrightarrow{DC} = \overrightarrow{FC}\)

   3. \(\overrightarrow{AE} + \overrightarrow{GB} + \overrightarrow{DH} = \overrightarrow{AE} + \overrightarrow{E...} + \overrightarrow{...} = \overrightarrow{...}\)

   \(\overrightarrow{AE} + \overrightarrow{GB} + \overrightarrow{DH} = \overrightarrow{AE} + \overrightarrow{EH} + \overrightarrow{HB} = \overrightarrow{AB}\)

2. Déterminer les sommes vectorielles suivantes :

   1. \(\overrightarrow{CH} + \overrightarrow{GE} = \overrightarrow{CH} + \overrightarrow{HD} = \overrightarrow{CD}\)

   2. \(\overrightarrow{AC} + \overrightarrow{EB} = \overrightarrow{FD} + \overrightarrow{DC} = \overrightarrow{FC}\)

   3. \(\overrightarrow{AE} + \overrightarrow{CB} + \overrightarrow{EB} = \overrightarrow{AE} + \overrightarrow{EF} + \overrightarrow{FA} = \overrightarrow{AA} = \overrightarrow{0}\)

   4. \(\overrightarrow{BA} + \overrightarrow{DC} - \overrightarrow{FE} = \overrightarrow{DE} + \overrightarrow{EB} - \overrightarrow{FE} = \overrightarrow{DB} + \overrightarrow{EF} = \overrightarrow{DB} + \overrightarrow{BA} = \overrightarrow{DA}\)

1.3 p 149 n° 124

Bien lire et faire le n° 123 avant.

1. Figure (ne pas la faire ici, ne pas l'envoyer...)

   

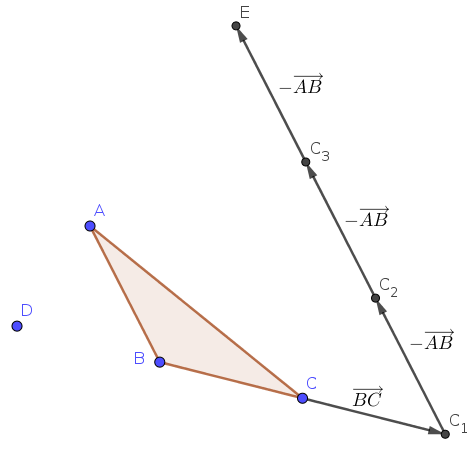
   p 149 n° 124

2. 1. \(\overrightarrow{AD} = \overrightarrow{A...} + \overrightarrow{C...}\)

   \(\overrightarrow{AD} = \overrightarrow{AC} + \overrightarrow{CD}\)

   2. Ecrire la série de calculs qui permet de montrer que : \(\overrightarrow{AD} = 2 \overrightarrow{AB} - \overrightarrow{AC}\) (ce doit donc être la dernière ligne de vore calcul).

   Souvent c'est plus simple de partir « de la partie à calculer » :
   

   \(2 \overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AB} + \overrightarrow{CA} = \overrightarrow{AB} + \overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{AB} + \overrightarrow{CB}\)

   Or \(D\) est le symétrique de \(C\) par rapport à \(D\), donc \(\overrightarrow{CB} = \overrightarrow{BD}\)

   D'où \(2 \overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BD} = \overrightarrow{AD}\)

   3. Ecrire la série de calculs qui permet de montrer que : \(\overrightarrow{AE} = -4 \overrightarrow{AB} + 2 \overrightarrow{AC}\) (ce doit donc être la dernière ligne de vore calcul).

   De la même façon que précédemment :

   \(- 4 \overrightarrow{AB} + 2 \overrightarrow{AC} = -3 \overrightarrow{AB} - \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AC} \\ = -3 \overrightarrow{AB} + \overrightarrow{BA} + \overrightarrow{AC} + \overrightarrow{AC} \\ = -3 \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{AC} \\ = \overrightarrow{CE} + \overrightarrow{AC} \\ = \overrightarrow{AC} + \overrightarrow{CE} \\ = \overrightarrow{AE}\)

3. Montrer que les points A, D et E sont alignés.

   On a montré que

   • \(\overrightarrow{AD} = 2\overrightarrow{AB} - \overrightarrow{AC}\)
   • \(\overrightarrow{AE} = -4 \overrightarrow{AB} + 2 \overrightarrow{AC}\)

   donc \(\overrightarrow{AE} = - 2 \overrightarrow{AD}\)

   Ce qui signifie que les vecteurs \(\overrightarrow{AE}\) et \(\overrightarrow{AD}\) sont colinéaires : donc les droites \((AE)\) et \((AD)\) sont parallèles, comme elles ont le points \(A\) en commun, elles sont confondues ; d'où le fait que les points \(A\), \(E\) et \(E\) soient alignés.