on sait que \(u_0 = -2\) et \(u_{n+1} = u_n + 1\)
Remarque la raison de la suite est \(1\), c'est pourquoi les termes vont de \(1\) en \(1\).
\(u_n = u_0 + n \times r\) donc ici : \(u_n = -2 + n\)
\(u_{25} = - 2 + 25 = 23\) (on remplace \(n\) par \(25\))
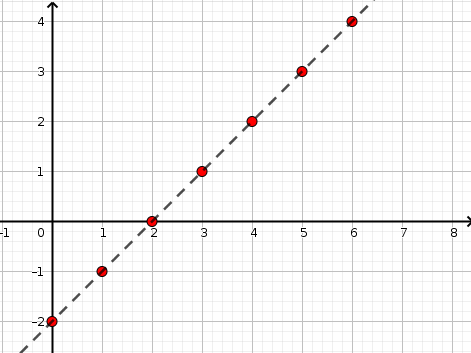(cours p. 42)
la raison de la suite est positive, donc la suite est croissante. (cours p. 42)
\(S_{25} = u_0 + u_1 + \dots + u_{25} = (1 + 25)\dfrac{u_0 + u_{25}}{2}\) (cours p. 44)
donc \(S_{25} = 26 \times \dfrac{-2 + 23}{2} = 273\)
\(3 n^2 + 7n - 4\,036 \geqslant 0\)
on reconnaît une inéquation du second degré de la forme \(a x^2+ bx + c\) avec \(a = 3\), \(b = 7\) et \(c = - 4\,036\).
comme \(a = 3\), la parabole associée est orientée « vers le haut »
on cherche les valeurs de \(x\) qui annulent l'équation :
calcul du discriminant : \(\Delta = b^2 - 4 ac\) \(\Delta = 48\,481\), donc il y a deux valeurs de \(x\) qui annulent l'équation :
\(\alpha = \dfrac{-b - \sqrt{\Delta}}{2 a} = \dfrac{-7 - \sqrt{48\,481}}{2 \times 3} \approx -37,9\)
et \(\beta = \dfrac{-b + \sqrt{\Delta}}{2 a} = \dfrac{-7 + \sqrt{48\,481}}{2 \times 3} \approx 35,5\)
Donc \(3 n^2 + 7n - 4\,036 \geqslant 0\) si \(n \in ]-\infty\,; \alpha]\) ou \(n \in [ \beta\,; +\infty[\).
Comme \(n\) est entier, il doit être dans \([ \beta\,; +\infty[\).
Conclusion : la somme est supérieure à \(2\,020\) si \(n\) est supérieur ou égal à \(36\).
Le corrigé du livre devrait suffire (c'est le même type d'exercice que p 69 n° 1).
La représentation de la suite est :
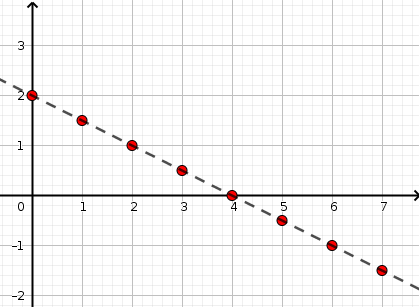(cours p. 42)
Remarque : c'est un exercice de livre de maths, dans la vraie vie ce type de contrat n'existe pas !!
Augmenter de \(1,5\,\%\) revient à multiplier par \(\left(1 + \dfrac{1,5}{100} \right)\), c'est à dire par \(1,015\).
donc
On passe d'un terme au suivant en multipliant par \(1,015\), c'est donc une suite géométrique (cours p. 45)
Comme le premier terme vaut \(u_0= 2\,000\) et la raison vaut \(1\,015\) donc \(u_n = 2\,000 \times 1,015^n\) (cours p. 46)
Juillet 2014 : on remarque que \(2014 = 2009 + 5\), on cherche donc \(u_5\) : \(u_5 = 2\,000 \times 1,015^5 \approx 2\,154,57\) Son salaire en juillet 2014 sera de \(2\,154,57\) euros.
C'est le même type d'exercice que p 76 n° 46, le corrigé du livre devrait suffire.
Le corrigé du livre devrait suffire.
La représentation de la suite est :
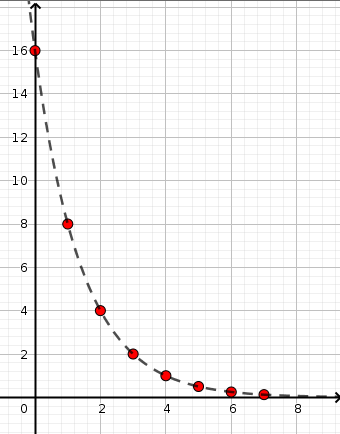(cours p. 47)
L'énoncé dit que \(u_0 = 50\,000\) ; \(u_1 = 48\,000\) et \(u_3 = 46\,080\).
Si la suite est géométrique cela signifie qu'il existe un réel \(q\) tel que \(u_1 = q \times u_0\) et \(u_2 = q \times u_1\).
Il faut donc que \(\dfrac{u_1}{u_0} = \dfrac{u_2}{u_1} = q\).
on calcule donc \(\dfrac{u_1}{u_0} = \dfrac{48\,000}{50\,000} = 0,96\) et \(\dfrac{u_2}{u_1} = \dfrac{46\,080}{48\,000} = 0,96\)
Les deux quotients sont égaux, donc \(q = 0,96\).
La suite \((u_n)\) est géométrique de raison \(0,96\).
La suite est géométrique donc (cours p. 46) : \(u_n = u_0 \times q^n = 50\,000 \times 0,96^n\).
On a donc \(u_{10} = 50\,000 \times 0,96^{10} \approx 33\,241,63\).
\(S_{10} = u_0 + u_1 + \dots = u_{10} = \dfrac{1 - 0,96^{10 + 1}}{1 - 0,96} \times 50\,000\) (cours p. 48) \(S_{10} \approx 452\,200,84\)
C'est le même exercice que p 72 n° 26... sauf que le premier terme est d'indice \(1\).
Donc réponses rapides : augmenter de \(10\,\%\) c'est multiplier par \(1,10\). 1.
C'est donc une suite géométrique de raison \(1,1\).
Expression de la suite : \(u_n = u_1 \times q^{n-1}\) (cours p. 46) soit \(u_n = 2\,000 \times 1,1^{n-1}\),
La production totale est \(S_{20} = u_1 + u_2 + \dots + u_{20} = \dfrac{1 - 1,1^{n}}{1 - 1,1} \times u_1\) (cours p. 48)
\(S_{20} = \dfrac{1 - 1,1^{20}}{1 - 1,1} \times 2\,000 \approx 114\,550\).
La production totale des 20 premières semaines est donc de \(114\,550\) système d'alarmes.