Exercices : Vecteurs et coordonnées

• p.135 nº11
• p.136 nº12
• p.137 nº16
• p.137 nº17
• p.150 nº134
• p.145 nº79
• p.151 nº142
• p.145 nº85

p.135 nº11

1. Placer les points / lire les coordonnées des vecteurs
   Aide

   
   Solution

   

   $\Vect{AB}\coor{7\\2}$ ; $\Vect{BC}\coor{1\\-5}$ $\Vect{CD}\coor{-7\\0}$ ; $\Vect{DA}\coor{-1\\3}$

p.136 nº12

1. Calculer les coordonnées des vecteurs.
   Aide

   Soient les points $A(\color{blue}{x_A}\,; \color{blue}{y_A})$ et $B(\color{red}{x_B} \,; \color{red}{y_B})$, alors $\Vect{\color{blue}{A}\color{red}{B}} \coor{\color{red}{x_B} - \color{blue}{x_A} \\ \color{red}{y_B} - \color{blue}{y_A} } $

   Remarque : même si l'énoncé ne le demande pas, on peut placer les points dans un repère pour s'aider !

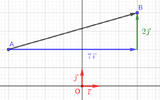
   Solution

   $\Vect{AB}\coor{\color{red}{3} - \color{blue}{1}\\ \color{red}{5} - \color{blue}{1}} = \coor{2 \\ 4}$

   $\Vect{DC}\coor{\color{red}{-3} - \color{blue}{(-5)}\\ \color{red}{2} - \color{blue}{(-2)}} = \coor{2 \\ 4}$

   Donc $\Vect{AB} = \Vect{DC}$ : le quadrilatère $ABCD$ est un parallélogramme.

p.137 nº16

1. Calculer les coordonnées des vecteurs.
   Aide

   Soient les points $A(\color{blue}{x_A}\,; \color{blue}{y_A})$ et $B(\color{red}{x_B} \,; \color{red}{y_B})$, alors $\Vect{\color{blue}{A}\color{red}{B}} \coor{\color{red}{x_B} - \color{blue}{x_A} \\ \color{red}{y_B} - \color{blue}{y_A} } $

   Remarque : même si l'énoncé ne le demande pas, on peut placer les points dans un repère pour s'aider !

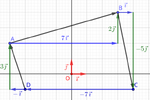
   Solution

   $\Vect{MN}\coor{\color{red}{23} - \color{blue}{2}\\ \color{red}{6} - \color{blue}{3}} = \coor{21 \\ 3}$

   $\Vect{PR}\coor{\color{red}{-10} - \color{blue}{4}\\ \color{red}{-5} - \color{blue}{(-3)}} = \coor{-14 \\ -2}$

   $\Vect{NR}\coor{\color{red}{-10} - \color{blue}{23}\\ \color{red}{-5} - \color{blue}{6}} = \coor{-33 \\ -11}$

   $\Vect{MP}\coor{\color{red}{4} - \color{blue}{2}\\ \color{red}{-3} - \color{blue}{3)}} = \coor{2 \\ -6}$

2. 1. parallélisme des droites $(MN)$ et $(PR)$
      Aide 1

      Dire que les droites $(MN)$ et $(PR)$ sont parallèles, revient à dire que les vecteurs $\Vect{MN}$ et $\Vect{PR}$ sont colinéaires

      Aide 2

      Dire que les vecteurs $\Vect{MN}$ et $\Vect{PR}$ sont colinéaires est équivalent à dire que leurs coordonnées sont proportionnelles.

      Solution

      $\begin{array}{lcc} & \Vect{MN} & \Vect{PR} \\\hline \text{abscisse} & 21 & -14 \\\hline \text{ordonnée} & 3 & -2 \\\hline \end{array}$

      $21 \times (-2) = 3 \times (-14)$ donc les coordonnées sont proportionnelles : les droites $(MN)$ et $(PR)$ sont parallèles.

   2. parallélisme des droites $(NR)$ et $(MP)$
      Solution

      $\begin{array}{lcc} & \Vect{NR} & \Vect{MP} \\\hline \text{abscisse} & -33 & 2 \\\hline \text{ordonnée} & -11 & -6 \\\hline \end{array}$

      $-33 \times (-6) \neq (-11) \times 2$ donc les coordonnées ne sont pas proportionnelles : les droites $(MN)$ et $(PR)$ sont sécantes.

p.137 nº17

1. Les points $H$, $K$ et $L$ sont-ils alignés ?
   Aide

   Dire que les points $H$, $K$ et $L$ sont alignés est équivalent à dire les vecteurs $\Vect{HK}$ et $\Vect{HL}$ sont colinéaires.

   Solution

   $\Vect{HK}\coor{\color{red}{17} - \color{blue}{8}\\ \color{red}{37} - \color{blue}{19}} = \coor{9 \\ 18}$

   $\Vect{HL}\coor{\color{red}{11} - \color{blue}{8}\\ \color{red}{25} - \color{blue}{19}} = \coor{3 \\ 6}$

   $\begin{array}{lcc} & \Vect{HK} & \Vect{HL} \\\hline \text{abscisse} & 9 & 3 \\\hline \text{ordonnée} & 18 & 6 \\\hline \end{array}$

   $9 \times 6 = 3 \times 18$, donc les vecteurs sont colinéaires, et les points $H$, $K$ et $L$ sont alignés.

2. Les points $H$, $K$ et $M$ sont-ils alignés ?
   Solution

   $\Vect{HM}\coor{\color{red}{-8} - \color{blue}{(-8)}\\ \color{red}{-14} - \color{blue}{19}} = \coor{0 \\ -33}$

   $\begin{array}{lcc} & \Vect{HK} & \Vect{HM} \\\hline \text{abscisse} & 9 & 0 \\\hline \text{ordonnée} & 18 & -33 \\\hline \end{array}$

   $9 \times (-33) \neq 18 \times 0$, donc les vecteurs ne sont pas colinéaires, et les points $H$, $K$ et $L$ ne sont pas alignés.

p.150 nº134

1. Coordonnées de $M$ tel que $\Vect{AM} = 3 \Vect{AB}$
   Aide

   Les vecteurs sont égaux si et seulement si leurs coordonnées sont égales.

   Solution

   $\Vect{AB} \coor{7 - (-3) \\ 9 - 2} = \coor{10 \\ 7}$

   donc $\color{red}{3}\Vect{AB}$ a pour coordonnées $\coor{\color{red}{3 \times }10 \\ \color{red}{3 \times } 7} = \coor{30 \\ 21}$

   $\Vect{AM} \coor{x - (-3) \\ y - 2} = \coor{x + 3 \\ y - 2}$

   On veut : $\left\lbrace\begin{array}{rl} x + 3 &= 30 \\ y - 2 &= 21 \end{array}\right. \ssi \left\lbrace\begin{array}{rl} x &= 27 \\ y &= 23 \end{array}\right.$

2. Coordonnées de $N$ tel que $\Vect{BN} = -5 \Vect{BC}$
   Solution

   $\Vect{BC} \coor{-5 - 7 \\ 4 - 9} = \coor{-12 \\ -5}$

   donc $\color{red}{-5}\Vect{BC}$ a pour coordonnées $\coor{\color{red}{-5 \times }(-12) \\ \color{red}{-5 \times } (-5)} = \coor{60 \\ 25}$

   $\Vect{BN} \coor{x - 7 \\ y - 9} $

   On veut : $\left\lbrace\begin{array}{rl} x - 7 &= 60 \\ y - 9 &= 25 \end{array}\right. \ssi \left\lbrace\begin{array}{rl} x &= 67 \\ y &= 34 \end{array}\right.$

3. Coordonnées de $P$ tel que $\Vect{CP} = 2 \Vect{AB} - 3 \Vect{AC}$
   Aide 1

   Soient les vecteurs $\vec{u}$ de coordonnées $\coor{x \\ y}$ et $\vec{u'}$ de coordonnées $\coor{x' \\ y'}$, alors le vecteur $\vec{u} + \vec{u'}$ a pour coordonnées $\coor{x + x' \\ y + y'}$
   Aide 2

   $\Vect{AB} \coor{7 - (-3) \\ 9 - 2} = \coor{10 \\ 7}$, donc $\color{red}{2} \Vect{AB} \coor{\color{red}{2 \times } 10 \\ \color{red}{2 \times} 7} = \coor{20\\14}$
   Solution

   $\Vect{AC} \coor{-5 - (-3) \\ 4 - 2} = \coor{-2 \\ 2}$, donc $\color{red}{-3} \Vect{AC} \coor{\color{red}{-3 \times } (-2) \\ \color{red}{-3 \times} 2} = \coor{6\\-6}$

   donc $2\Vect{AB} - 3 \Vect{AC} \coor{20 + 6 \\ 14 - 6} = \coor{26 \\ 8}$

   $\Vect{CP} \coor{x_P - (-5) \\ y_P - 4} = \coor{x_P + 5 \\ y_P - 4}$

   On veut $\left\lbrace\begin{array}{rl} x_P + 5 = 26 \\ y_P - 4 = 8 \end{array}\right. \ssi \left\lbrace\begin{array}{rl} x_P = 21 \\ y_P = 12 \end{array}\right.$

p.145 nº79

1. $\vec{u} \coor{2 \\ -3}$ et $\vec{v} \coor{25 \\ t}$ : déterminer la valeur de $t$ telle que les vecteurs $\vec{u}$ et $\vec{v}$ soient colinéaires.
   Aide

   Les vecteurs sont colinéaires si et seulement si leurs coordonnées sont proportionnelles.

   Solution

   On veut : $2 \times t = 25 \times (-3) \ssi t = -\dfrac{75}2$

p.151 nº142

1. Expression du vecteur $\Vect{BM}$ en fonction du vecteur $\Vect{BC}$
   Solution

   $M$ est le milieu de $[BC]$, donc $\Vect{BM} = \dfrac12 \Vect{BC}$

2. Coordonnées des points $M$, $D$ et $E$.
   Aide 1

   Si le vecteur $\Vect{AB}$ de coordonnées $\coor{x_B - x_A \\ y_B - y_A}$ est égal à $k \times \vec{u}$ avec $\vec{u}$ de coordonnées $\coor{x_0 \\ y_O}$, alors on a $\left\lbrace\begin{array}{lr} x_B - x_A = k x_0 \\ y_B - y_A = k y_0 \end{array}\right.$

   Aide 2

   $\Vect{BM} = \dfrac12 \Vect{BC}$ avec $\Vect{BM} \coor{x_M - x_B \\ y_M - y_B}$ et $\Vect{BC} \coor{-2 \\ 6}$

   Donc il faut : $\left\lbrace\begin{array}{lr} x_M - x_B = \ffrac12 \times (-2)\\ y_M - y_B = \ffrac12 \times 6 \end{array}\right.$

   Solution

   • point $M$

     $\Vect{BM} = \dfrac12 \Vect{BC}$ avec $\Vect{BM} \coor{x_M - x_B \\ y_M - y_B}$ et $\Vect{BC} \coor{-2 \\ 6}$

     Donc il faut : $\left\lbrace\begin{array}{lr} x_M - 5 = \ffrac12 \times (-2)\\ y_M - (-1) = \ffrac12 \times 6 \end{array}\right. \ssi \left\lbrace\begin{array}{lr} x_M = 4\\ y_M = 2 \end{array}\right. $

   • point $D$

     $\Vect{AD} = \dfrac32 \Vect{AB}$ avec $\Vect{AD} \coor{x_D - 1 \\ y_D - 1}$ et $\Vect{AB} \coor{4 \\ -2}$

     Donc il faut : $\left\lbrace\begin{array}{lr} x_D - 1 = \dfrac32 \times 4\\ y_D - 1 = \dfrac32 \times (-2) \end{array}\right. \ssi \left\lbrace\begin{array}{lr} x_D = 7\\ y_D = -2 \end{array}\right. $

   • point $E$

     $\Vect{AE} = \dfrac34 \Vect{AC}$ avec $\Vect{AE} \coor{x_E - 1 \\ y_E - 1}$ et $\Vect{AC} \coor{2 \\ 4}$

     Donc il faut : $\left\lbrace\begin{array}{lr} x_E - 1 = \dfrac34 \times 2\\ y_E - 1 = \dfrac34 \times 4 \end{array}\right. \ssi \left\lbrace\begin{array}{lr} x_E = \dfrac52\\ y_E = 4 \end{array}\right. $

3. Alignement des points $E$, $M$ et $D$.
   Aide

   Dire que les points $E$, $M$ et $D$ sont alignés est équivalent à dire que les vecteurs $\Vect{EM}$ et $\Vect{MD}$ sont colinéaires.

   Solution

   $\Vect{EM} \coor{4 - \ffrac52 \\ 2 - 4} = \coor{\ffrac32 \\ -2}$

   $\Vect{MD} \coor{7 - 4 \\ -2 - 2} = \coor{3 \\ -4}$

   On remarque que $\ffrac32 \color{red}{\times 2 } = 3$ et que $-2 \color{red}{\times 2 } = -4$ ; donc $\color{red}{2} \Vect{EM} = \Vect{MD}$ : les vecteurs sont colinéaires ; donc les points $E$, $M$ et $D$ sont alignés.

p.145 nº85

1. 1. Colinéatrité des vecteurs $\Vect{AB}$ et $\Vect{CD}$.
      Aide 1

      Les vecteurs sont colinéaires si et seulement si leurs coordonnées sont proportionnelles.

      Aide 2

      Il est prudent de faire une figure... cela peut aider à vérifier !

      
      Solution

      $\Vect{AB}\coor{\color{red}{2} - \color{blue}{(-1)}\\ \color{red}{3} - \color{blue}{4}} = \coor{3 \\ -1}$

      $\Vect{CD}\coor{\color{red}{6} - \color{blue}{(-3)}\\ \color{red}{-2} - \color{blue}{1}} = \coor{9 \\ -3}$

      $\begin{array}{lcc} & \Vect{AB} & \Vect{CD} \\\hline \text{abscisse} & 3 & 9 \\\hline \text{ordonnée} & -1 & -3 \\\hline \end{array}$

      $3 \times (-3) = (-1) \times 9$, donc les vecteurs sont colinéaires.

   2. Nature de $ABCD$.
      Aide

      Dire que des vecteurs sont colinéaires, est équivalenbtà dire que les droites qui les portent sont parallèles.

      Un trapèze est un quadrilatère qui a deux côtés parallèles.

      Solution

      Les vecteurs $\Vect{AB}$ et $\Vect{CD}$ sont colinéaires, donc les droites $(AB)$ et $(CD)$ sont parallèles : le quadrilatère $ABDC$ est donc un trapèze.

2. Alignement des points $C$, $O$ et $D$.
   Aide

   Dire que les points $C$, $O$ et $D$ sont alignés est équivalent à dire que les vecteurs $\Vect{OC}$ et $\Vect{OD}$ sont colinéaires.

   Solution

   $\Vect{OC}\coor{\color{red}{-3} - \color{blue}{0}\\ \color{red}{1} - \color{blue}{0}} = \coor{-3 \\ 1}$

   $\Vect{OD}\coor{\color{red}{6} - \color{blue}{0}\\ \color{red}{-2} - \color{blue}{0}} = \coor{6 \\ -2}$

   On remarque que $2 \times \Vect{OC} = \Vect{OD}$, donc les vecteurs $\Vect{OC}$ et $\Vect{OD}$ sont colinéaires : les points $O$, $C$ et $D$ sont alignés.

3. Nature de $OCAB$.
   Aide

   Placer le spoints dans un repère : $OCAB$ semble être un parallélogramme.

   Un parallélogramme peut être défini par une égalité de deux vecteurs.

   Solution

   Le vecteur $\Vect{AB}$ a pour coordonnées $\coor{3 \\ -1}$ ; le vecteur $\Vect{CO}$ est l'opposé du vecteur $\Vect{OC}$, donc ses coordonnées sont $\coor{3 \\ -1}$.

   donc $\Vect{AB} = \Vect{CO}$ : le quadrilatère $OCAB$ est un parallélogramme.