Python, représentation graphique, probabilités

La méthode de Monte-Carlo pour estimer une surface : travail sur les lunules d'Hyppocrate

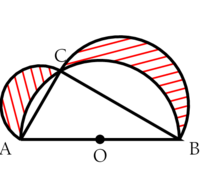
1. Calculer la somme de l'aire des lunules.
2. On suppose que dans la première figure $AO = AC$, en déduire $BC$, puis d'aire de $ABC$.

from math import sqrt

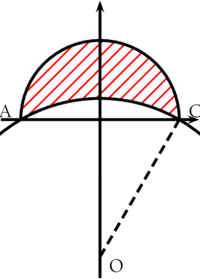
1. Pour calculer l'aire de la lunule de diamètre $[AC]$, on se place dans un repère est orthonormé avec $A(-1\,; 0)$, $C(1\,; 0)$ et $O \left(0 \,; - \frac{\sqrt{3}}{2}\right)$.
   Donc le cercle $\mathscr C_1$ de diamètre $[AC]$ a pour équation $x^2 + y^2 - 1 = 0$ et le cercle $\mathscr C_0$ de centre $O$ a pour équation $x^2 + (y + \sqrt{3})^2 = 4$.
   On cherche a estimer l'aire de la lunule à l'aide de la méthode de Monte-Carlo en plaçant des points au hasard dans $[-1\,; 1] \times [0\,; 1]$

from matplotlib import pyplot as plt   # bibliothèque pour les graphiques
from random import uniform             # bibliothèque pour les nombres au hasard
from math import sqrt                  # bibliothèque pour les fonctions mathématiques

def est_dansC1(x,y):
    """retourne True si le point est dans le cercle de diamètre [AC]"""
    if x**2 + y**2 - 1 < 0:
        return True
    else:
        return False

def est_dansC0(x,y):
    """retourne True si le point est dans le cercle de centre O"""
   ...

    
n = 50000
x_rouge, y_rouge = [],[]    # création de listes de valeurs
x_bleu, y_bleu = [],[]
eff_rouge1 = 0

for _ in range(n):
    x = uniform(-1,1)
    y = uniform(0,1)
    if ...
        x_rouge.append(x)
        y_rouge.append(y)
        eff_rouge1 += 1   # eff_rouge1 = eff_rouge1 + 1
    else:
        ...
        
plt.plot(x_rouge, y_rouge,'r.')
plt.plot(x_bleu, y_bleu,'b.')
plt.show()

1. En déduire une estimation de l'aide de la lunule.

1. Procéder de la même façon pour obtenir une estimation de l'aide de la lunule de diamètre $[BC]$

def est_dansC2(x,y):
    """retourne True si le point est dans le cercle de diamètre [BC]"""
    ...

def est_dansC0(x, y):
    # l'équation de c0 n'est pas la même dans ce repère !
    # Python redéfini la fonction sans avertissement...
    ...
    
# n est déjà défini, mais il faut réinitiliser les listes
x_rouge ...
x_bleu ...
eff_rouge2 = 0

for _ in range(n):
    ...
        
plt.plot(x_rouge, y_rouge,'r.')
plt.plot(x_bleu, y_bleu,'b.')
plt.show()

# estimation de la somme des aires des lunules

Travail sur le typage et la récursivité

2019 est un nombre heureux !

$2019 \Rightarrow 2^2 + 0^2 + 1^2 + 9^2 = 86 \Rightarrow 8^2 + 6^2 = 100 \Rightarrow 1^2 + 0^2 + 0^2 = 1$

1. Quelle est la prochaine année heureuse ?
2. Lister les $n$ premièrs nombres heureux.