Rappels de cours

quelques fonctions dérivées

\(f(x)= mx + p \) alors \( f'(x) = m \)
\(f(x)= x^2 \) alors \( f'(x) = 2x \)
\(f(x)= a x^2 + b x + c \) alors \( f'(x) = 2ax + b \)
\(f(x)= x^3 \) alors \( f'(x) = 3x^2 \)
\(f(x)= \sqrt{x} \) alors \( f'(x) = \dfrac1{2\sqrt{x}} \)
\(f(x)= \dfrac1x \) alors \( f'(x) = - \dfrac1{x^2} \)

équation de la tangente

\( y = f'(a) (x-a) + f(a) \)

Opérations avec les fonctions dérivées

somme / différence de deux fonctions

si \( f(x) = \color{blue}{x^2} + \color{red}{bx + c} \) elle est de la forme \(ax^2 + bx + c\) avec \(a = 1\)

On a démontré que \( f'(x) = 2ax + b \), donc ici : \( f'(x) = 2x + b \)

on remarque que \( f(x) \) peut s'écrire sous la forme \( f(x) = u(x) + v(x) \) avec \( \color{blue}{u(x)= x^2} \) et \( \color{red}{ v(x) = bx + c }\)

On a démontré que \( \color{blue}{u'(x)= 2x} \) et \( \color{red}{ v'(x) = b }\)

on remarque que \( f'(x) = \color{blue}{u'(x)} + \color{red}{v'(x)} \)

Règle : si \( f(x) = \color{blue}{u(x)} + \color{red}{v(x)} \) alors \( f'(x) = \color{blue}{u'(x)} + \color{red}{v'(x)} \)

produit par un réel

si \(f(x) = ax^2 \) elle est de la forme \(ax^2 + bx + c\) avec \(b = 0 \,; c=0\)

On a démontré que \( f'(x) = 2ax + b \), donc ici : \( f'(x) = 2ax = a \times 2x \)

on remarque que \( f(x) \) peut s'écrire sous la forme \( f(x) = \color{purple}{k}u(x) \) avec \( \color{purple}{k = a} \) et \( \color{red}{ u(x) = x^2 }\)

Règle : si \( f(x) = \color{purple}{k} \times \color{red}{u(x)} \) alors \( f'(x) = \color{purple}{k} \times \color{red}{u'(x)} \)

page 105 n° 1

\(f(x) = 3x - 4\)

fonction affine \( x \mapsto mx + p\) avec \( m = 3\) et \( p = -4\). La dérivée est de la forme \( x\mapsto m\).
donc \(f'(x) = 3\)

\( g(x) = (2x + 1)^2 \)

il faut d'abord développer !
\( g(x) = 4x^2 + 4x + 1\) de la forme \(x \mapsto ax^2 + bx + c\) avec \(a = 4\,; b = 4\) et \(c = 1\)
donc \(g'(x) \) est de la forme \( x \mapsto 2ax + b \) d'où \(g'(x) = 2 \times 4 x + 4 = 8x + 4 \)

\( h(t) = 5 t^3 - 3 t^2 + t - \sqrt2 \)

\( h(t) = \color{blue}{ 5 t^3} + \left(\color{red}{ - 3 t^2 + t - \sqrt2 }\right)\)

\(u(t) = \color{blue}{ 5 t^3}\) de la forme \( t \mapsto \color{green}{5} \times t^3\)
donc \(u'(t) = \color{green}{5} \times 3 t^2= 15 t^2\)

\(v(t) = \color{red}{ - 3 t^2 + t - \sqrt2 }\) de la forme \( t \mapsto at^2+ bt + c\) avec \(a = -3 \,; b = 1\) et \(c = -\sqrt2\)
donc \(v'(t) \) est de la forme \(t \mapsto 2at+ b\) d'où \( v'(t) = 2 \times (-3) t + 1 = - 6t + 1\)
donc \(h'(x) = u'(t) + v'(t)\)
\( h'(t) = 15 t^2 - 6 t + 1\)

\( i(x) = \dfrac{x}2 - \dfrac3x \)

\( i(x) = \color{blue}{ \dfrac12 x} + \color{red}{(-3)\dfrac1x}\)

\(\color{blue}{u(t)} = \dfrac12 x\) de la forme \( x \mapsto mx + p\) avec \( m = \dfrac12 \) et \( p = 0 \)
donc \(u'(t) \) de la forme \( x \mapsto m \) d'où \( u'(x) = \dfrac12 \)

\(\color{red}{v(t)} = \color{green}{ ( - 3)} \times \dfrac1x \) de la forme \( x \mapsto \color{green}{k} \times w(x)\) avec \( k=-3 \) et \(w(x) = \dfrac1x\)
donc \(v'(t) = \color{green}{-3} \times \dfrac{-1}{x^2} = \dfrac3{x^2}\)
donc \(i'(x) = \color{blue}{u'(t)} + \color{red}{v'(t)}\)
\( i'(t) = \color{blue}{\dfrac12} + \color{red}{\dfrac3{x^2}} \)

\( j(x) = \dfrac{x^2 - 4}2 \)

\( j(x) = \dfrac{x^2}2 - 2 = \dfrac12 x^2 - 2\)

\(j\) est de la forme \( x \mapsto ax^2 + bx + c\) avec \( a = \dfrac12 \,; b = 0 \) et \( c = -2 \)
donc \(j'(x) \) de la forme \( x \mapsto 2ax + b \) d'où \( j'(x) = 2 \times \dfrac12 x + 0 = x \)

\( k(x) = 2x^3 - 4\sqrt{x} \)

\( k(x) = \color{blue}{ 2x^3} + \color{red}{(-4)\sqrt{x}}\)

\(\color{blue}{u(x)} = \color{green}{2} x^3\) de la forme \( x \mapsto \color{green} u_1(x)\) avec \( k = 2 \) et \( u_1(x) = x^3 \)
donc \(u'(t) \) de la forme \( x \mapsto \color{green}{k} u_1'(x) \) d'où \( u'(x) = \color{green}{2} \times 3 x^2 = 6 x^2 \)

une erreur dans ce corrigé !?! -> plus maintenant ! Grâce à vous...
\(\color{red}{v(t)} = \color{green}{ ( - 4)} \times \sqrt{x} \) de la forme \( x \mapsto \color{green}{k} \times v_1(x)\) avec \( k=-4 \) et \(v_1(x) = \sqrt{x}\)
donc \(v'(t) = \color{green}{-4} \times \dfrac{1}{2\sqrt{x}} = -\dfrac{2}{\sqrt{x}}\)
donc \(k(x) = \color{blue}{u'(t)} + \color{red}{v'(t)}\)
\( k'(x) = \color{blue}{6x^2} - \color{red}{\dfrac{2}{\sqrt{x}}} \)

page 116 n° 33 (1 et 2)

\(f(t) = 2t - \dfrac1t\)

\( f(t) = \color{blue}{2t} - \color{red}{\dfrac1t}\) : posons \( u(t) = \color{blue}{2t}\) et \(v(t) = \color{red}{\dfrac1t}\)

\( u \) est de la forme \(t \mapsto mt + p \)avec \(m = 2\) et \(p=0\), donc \(u'(t) = \color{blue}{2}\).

la dérivée de \( t \mapsto \dfrac1t\) est \( x \mapsto -\dfrac1{t^2}\), donc \( v'(t) = \color{red}{-\dfrac1{t^2}}\)
on en déduit que \(f'(t) = \color{blue}{u'(t)} - \color{red}{v'(t)} \) ; donc \(f'(t) = \color{blue}{2} - \left( \color{red}{-\dfrac1{t^2}} \right)\)
\(f'(t) = 2 + \dfrac1{t^2}\)

\( f(x) = 5\sqrt{x} - 3x + 2 \)

\( f(x) = \color{blue}{5\sqrt{x}} + \left( \color{red}{- 3x + 2}\right) \)
somme de deux fonctions : une de la forme \(x \mapsto \color{green}{k}\sqrt{x}\) et une affine.
donc \(f'(x) = \dfrac5{2\sqrt{x}} - 3\)

Exercice type pour le contrôle

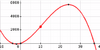
Soit la fonction \( f(x) = -\dfrac23 x^3 + 22x^2 + 96x \) définie sur \( \mathbb R\) et \( \mathscr C\) sa courbe représentative.

À l'aide de la calculatrice, donner une allure de \( \mathscr C\) et préciser les abscisses des extréma.
- schéma reprenant les éléments de cette image
- On lit que la fonction admet un maximum local pour \( x \approx 24\) et un minimum local pour \( x= -2 \)
Déterminer la dérivée de la fonction \(f\) en remarquant que \(f(x) = \color{blue}{-\dfrac23 x^3} + \color{red}{22x^2 + 96x}\)
Aide
- \(x \mapsto -\dfrac23 x^3\) est de la forme \(x \mapsto \color{gree}{k} u(x) \) avec \(\color{gree}{k = -\dfrac23}\) et \(u(x) = \dots\)
- \( \color{red}{22x^2 + 96x}\) est de la forme \( x \mapsto ax^2 + bx + c \), donc ...
Solution
\(f'(x) = -2 x^2 + 44x + 96 \)
Déterminer les valeurs exactes des abscisses des extrema.

Aide
Quand la fonction atteint un extremum local, la tangente à la courbe est parallèle à l'axe des abscisses, donc sa pente est nulle. Autrement dit, on cherche \(x\) tel que \(f'(x) = 0\)

Solution

\(f'(x) = 0 \Leftrightarrow -2 x^2 + 44x + 96 = 0\)

méthode rapide : on remarque que \(x = -2\) est une racine (évidente), donc l'autre est \(24\) car le produit des racines est \(\dfrac{96}{-2} = - 48\).

méthode longue : \( f'(x) =ax^2 + bx + c \) avec \(a = \dots \,; b = \dots \)
calcul du discriminant : \(\Delta = b^2 - 4ac\), puis calcul des racines.

la fonction admet un minimum pour \(x=-2\) et un maximum pour \(x=24\).
Soit la fonction \(g\) définie sur \( \mathbb R\) par \(g(x) = x^3 - 34,5 x^2 - 150 x + 90\).
Les fonctions \(f\) et \(g\) admettent-elles des extrema de même abscisse ?

Aide

Quand la fonction atteint un extremum local, la tangente à la courbe est parallèle à l'axe des abscisses, donc sa pente est nulle. Autrement dit, on cherche \(x\) tel que \(g'(x) = 0\).

Puis comparer les valeurs obtenues avec celles de \(f\).

Solution

Cette question est un test pour repérer ceux d'entre vous qui ont cherché ;-) Réponse lundi !