Comptine géométrique
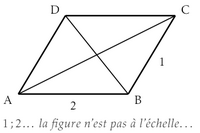
Un, Deux
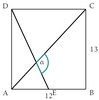
Il faut calculer $AC^2 + BD^2$.
On peut introduire les points H et I tels que H soit le projeté orthogonal de C sur la droite (AB) et I est celui de B sur la droite (DC).
clique ici pour écrire la somme des carrés des diagonales.
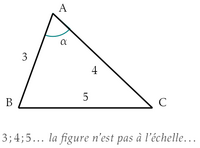
Trois, Quatre, Cinq...
Ne serait-ce pas un triangle particulier ?
clique ici pour écrire la valeur en radians de $\alpha$ (pour $\dfrac{3\pi}4$ écrire «3PIsur4»)
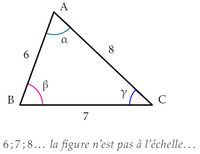
Six, Sept, Huit...
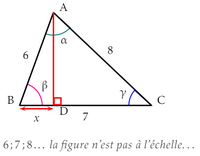
Pour trouver la valeur de $x$ :
- triangle ADB : $AD^2 = 6^2 - x^2$
- triangle ADC : $AD^2 = 8^2 - (7 - x)^2$
Puis trouver les valeurs de $\beta$ et $\gamma$ à l'aide de la fonction $\acos$.
La somme des angles est $\pi$ radians.
clique ici pour écrire la partie décimale de $\cos \beta$.
Neuf, Dix, Onze...
Position relative des droites $D_1$ et $D_2$
- $D_1 : 10x - 9y + 11 = 0 $
- $D_2 : 10x + 11y - 9 = 0 $
- Donner les expressions réduites des droites, en déduire qu'elles sont sécantes en un point A (utiliser la colinéarité des vecteurs directeurs).
- Définir les points B et C correspondants à l'intersection des droites avec l'axe des ordonnées.
- Déterminer la nature du triangle ABC.
Droites sécantes
- $D_1 : y = \dfrac{10}9 x + \dfrac{11}9$ de vecteur directeur $\vec{u_1} \dbinom1{\frac{10}9}$ et $D_2 : y = -\dfrac{10}{11} x + \dfrac{9}{11}$ de vecteur directeur $\vec{u_2} \dbinom1{-\frac{10}{11}}$
- Rappel : les vecteurs $\vec{u} \dbinom{x}{y}$ et $\vec{v} \dbinom{x'}{y'}$ sont colinéaires (et donc les droites sont parallèles) si et seulement si leurs coordonnées sont proportionnelles, c'est à dire si $x y ' - x' y = 0$
- ici : $1 \times \left( -\dfrac{9}{11} \right) - \dfrac{10}9 \times 1 \neq 0$, donc les droites ne sont pas parallèles (elles sont sécantes).
Coordonnées de A
Le point A appartient aux deux droites, donc ses coordonnées vérifient : $\left\lbrace\begin{array}{rl@{\quad}l} 10x - 9y + 11 &= 0 & L_1 \\ 10x + 11y - 9 &= 0 & L_2 \\ \end{array}\right. \Leftrightarrow \left\lbrace\begin{array}{rl@{\quad}l} x &= \dfrac{9y - 11}{10} & L_1 \gets L_1 \\ 20y - 20 &= 0 & L_2 \gets L_2 - L_1 \\ \end{array}\right. \Leftrightarrow \left\lbrace\begin{array}{rl@{\quad}l} x &= -0,2 \\ y &= 1 & \\ \end{array}\right.$
Coordonnées de B et C
$B$ est le point d'intersection de $D_1$ avec l'axe des abscisses : $B\left( 0\,; \dfrac{11}9 \right)$ ; $C$ est le point d'intersection de $D_2$ avec l'axe des abscisses : $C\left( 0\,; \dfrac9{11} \right)$
les droites sont perpendiculaires si et seulement si $AB^2 + AC^2 = BC^2 $.
clique ici pour écrire le numérateur de la fraction réduite de $AB^2 + BC^2$.
Douze, Treize !
13 ! Quelle chance : on connaît le produit scalaire !
si on ne connaît pas le produit scalaire :
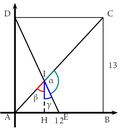
- $I$ est l'intersection de $(AC)$ et $(DE)$
- Dans un repère orthonormé tel que $A(0\,;0)$, $B(12\,;0)$ et $D(0\,;13)$, déterminer les coordonnées du point $I$.
- $H$ est le projeté orthogonal de $I$ sur (AB)
- Déterminer les équations des droites $(AC)$ et $(DE)$ ; en déduire les coordonnées du point $I$
- Calculer $\tan \beta$ et $\tan\gamma$ ; en déduire les valeurs approchées de $\beta$ et $\gamma$.
- Conclure en calculant la valeur de $\alpha$.
- $(DE) : y = - \dfrac{13}6 x + 13$ et $(AC) : y = \dfrac{13}{12} x$.
- $I \left( 4\,; \dfrac{13}3 \right)$.
clique ici pour écrire la partie entière de l'angle $\alpha$ mesuré en degré.