Fermat : p. 134

Soit le segment \([AC]\). Déterminer la position du point \(E\) sur \([AC]\) telle que le rectangle de longueur \(AE\) et de largeur \(EC\) ait une aire maximale.

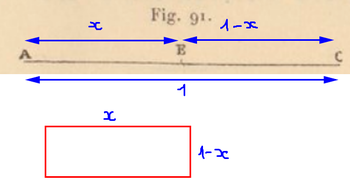
modélisation pb page 134

Soit \(\mathscr A\) l'aire du rectangle : \(\mathscr A(x) = (1 -x) \times x\) avec \(x = AE\), donc \(x \in [0\,;1]\)

On cherche \(x\) tel que \(\mathscr A(x)\) soit maximale.

\(\mathscr A(x) = x - x^2\)

on reconnaît un polynôme de degré 2 (de la forme \(ax^2+ bx + c\)) avec \(a=-1\), \(b=1\) et \(c=0\). Comme \(a<0\) la sommet de la parabole représente le maximum de la fonction. L'abscisse du maximum est donné par \(x_0 = - \dfrac{b}{2a} = \dfrac12\)

remarque géométrique : de tous les rectangles de même périmètre, celui qui a la plus grand surface est le carré.

Fermat : p 140

Soit le segment \([AC]\). Déterminer la position du point \(B\) sur \([AC]\) telle que le solide ayant pour base le carré de côté \(AB\) et de hauteur la longueur \(BC\) ait un volume maximal.

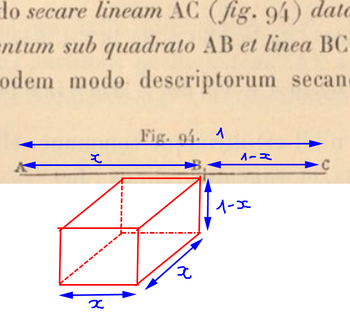
modélisation pb page 140

posons \(\mathscr V(x)\) le volume du solide, avec \(x = AB\) et \(x \in [0\,;1]\).

\(\mathscr V(x) = x \times x \times (1 - x)\)

à faire :

• expression développée
• tracer la fonction à l'aide un logiciel
• lire les coordonnées du maximum