Fermat : pb du volume
\(x \in [0\,;1]\) ; on cherche \(x\) tel que \(V(x) = x^2 (1- x)\) soit maximal.
lecture graphique
On lit que le volume est maximum pour \(x \approx 0,66\) et il vaut environ \(0,15\)
Idée des tangentes
- tangente à un cercle : c'est une droite perpendiculaire au rayon.
- question : tangente à la courbe d'une fonction ?
la notion de tangente est locale (la droite est tangente à la courbe autour du point)
- si la tangente passe par un minimum (ou un maximum) local, la tangente est parallèles à l'axe des abscisses.
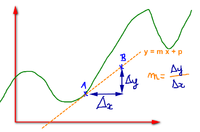
- un tangente, c'est une droite, donc son équation est de la forme \(y = mx +p\) (rappel : \(m\) est le coefficient directeur et \(p\) est l'ordonnée à l'origine)
- si la tangente passe par un minimum (resp. maximum) local, alors son coefficient directeur est nul.
Comment calculer le coefficient directeur de la tangente ?
Si l'équation de la droite est \(y = mx +p\) et que les points \(A(x_A\,; y_A)\) et \(B(x_B\,; y_B)\) appartiennent à la droite, on sait que :
\(m = \dfrac{\Delta_y}{\Delta_x} = \dfrac{y_B - y_A}{x_B - x_A}\)
L'idée : rapprocher le point \(M\) du point \(A\), donc \(x_M\) est "très proche" de \(x_A\), de même \(y_M\) est "très proche" de \(y_A\). Ainsi \(\dfrac{y_B - y_A}{x_B - x_A}\) donnera la valeur du coefficient directeur de la tangente à la courbe en \(A\).
La notion d'infiniment petit
Comment calculer avec des réels très proches de \(0\) ?
exemples :
- \(\Delta_y = 10^{-100}\) et \(\Delta_x = 10^{-60}\), alors \(m=\dfrac{\Delta_y}{\Delta_x} = \dfrac{10^{-100}}{10 ^{-60}} = 10^{-100 - (-60)} = 10^{-40}\)
\(\Delta_y = 10^{-60}\) et \(\Delta_x = 10^{-100}\), alors \(m=\dfrac{\Delta_y}{\Delta_x} = \dfrac{10^{-60}}{10 ^{-100}} = 10^{-60 - (-100)} = 10^{40}\)
\(\Delta_y = 2 \times 10^{-60}\) et \(\Delta_x = 10^{-60}\), alors \(m=\dfrac{\Delta_y}{\Delta_x} = \dfrac{2 \times 10^{-60}}{10 ^{-60}} = 2\)
calcul du coefficient directeur de la tangente à la courbe au point A d'abscisse \(a\).
la formule du coefficient directeur serait \(\dfrac{y_M - y_A}{x_M - x_A}\) or ici on a \(A (a\,; f(a))\) et \(M(a + h\,; f(a + h))\) la formule devient : \(\dfrac{f(a + h) - f(a)}{(a + h) - a} =\dfrac{f(a + h) - f(a)}{h}\)
Pour indiquer que \(h\) est très, très; très petit on note :
\(\lim\limits_{h \to 0} \dfrac{f(a + h) - f(a)}{h} = f'(a)\)
\(f'(a)\) est le nombre dérivé de \(f\) en \(a\) et il représente le coefficient directeur de la tangente à la courbe de \(f\) au point d'abscisse \(a\).
Remarque : \(f'(a)\) n'existe pas à chaque fois. En effet \(f'(a)\) doit être un réel, c'est à dire il doit appartenir à \(]-\infty\,; +\infty[\); parfois on trouvera \(f'(a) = \pm\infty\) et d'autre fois suivant l'arrivée du point \(M\) (vers la gauche ou la droite du point \(A\)), on trouvera différentes valeurs.