Frédéric Léon -- MATHS -- E. Brontë

▲

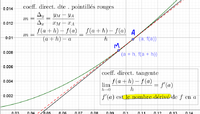
nombre dérivé : propriété

le nombre dérivé de la fonction \(f\) au point d'abscisse \(a\) se note \(f'(a)\) et il représente le coefficient directeur de la tangente à la courbe au point \(A(a\,; f(a))\)

Si \(A\) représente un minimum (maximum) local, alors la tangente en \(A\) est parallèle à l'axe des abscisses, son coefficient directeur est nul. C'est à dire \(f'(a) = 0\).

calculer le coeff directeur de la tangente

Fermat : volume maximal

théorie

pour \(x \in [0\,; 1]\), on a \(V(x) = x^2 -x^3\). On cherche \(x = a\) tel que le volume soit maximal, on cherche \(a\) tel que \(V'(a) = 0\).

Pour calculer \(V'(a)\) il faut :

calculs

1ere étape : simplifier le quotient

\(V(a + h) = (a + h)^2 - (a + h)^3\)

\(V(a + h) = a^2 + 2 ah + h^2 - (a^3 + 3 a^2 h + 3 a h^2 + h^3)\)

\(V(a + h) = a^2 + 2 ah + h^2 - a^3 - 3 a^2 h - 3 a h^2 - h^3\)

et \(V(a) = a^2 - a^3\)

donc (en factorisant suivant les puissances de \(h\)) : \(V(a + h) - V(a) = h (2a - 3 a^2) + h^2(1 - 3a) -h^3\)

donc \(\dfrac{V(a + h) - V(a)}{h} = \dfrac{h (2a - 3 a^2) + h^2(1 - 3a) -h^3}{h}\)

\(= \dfrac{h (2a - 3 a^2)}{h} + \dfrac{h^2(1 - 3a)}{h} - \dfrac{h^3}{h}\)

\(= (2a - 3 a^2) + h(1 - 3a) - h^2\)

limite quand \(h\) tends vers \(0\).

\(\lim\limits_{h \to 0} h^2 = 0\)

\(\lim\limits_{h \to 0} h(1 - 3a) = 0\)

\(\lim\limits_{h \to 0} 2a - 3a^2 = 2a - 3a^2\)

donc : \(\lim\limits_{h \to 0} \dfrac{V(a + h) - V(a)}{h} = 2a - 3a^2 = V'(a)\)

conclusion

On cherche \(a\) telle que \(V'(a) = 0\)

C'est à dire : \(2a - 3a^2 = 0\)

\(\Leftrightarrow a (2 - 3a) = 0\)

\(\Leftrightarrow a = 0 \text { ou } a= \dfrac23\).

C'est à dire le volume sera maximal pour \(x=\dfrac23\) et il vaudra \(V\left(\dfrac23\right) = \dfrac{4}{27}\)