profil altimétrique

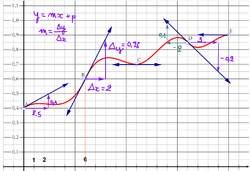
par lecture graphique : le coefficient directeur de la tangente à la courbe passant par le point \(B\) est

\(m_B = \dfrac{\Delta_y}{\Delta_x} = \dfrac{0,26}{2} = 0,13\)

Le coefficient directeur de la tangente s'appelle le nombre dérivé, ici \(f'(6) = 0,13\)

point \(A\) : l'abscisse de \(A\) est \(0\), on lit \(f'(0) = \dfrac{0,1}{2,5} = 0,04\)

point \(C\) : l'abscisse de \(C\) est \(11\) donc \(f'(11) = 0\)

point \(D\) : l'abscisse de \(D\) est \(16\), donc \(f'(16) = \dfrac{-0,2}{3} = -0,067\) ou bien (partie verte) : \(f'(16) = \dfrac{0,1}{-2} = -0,05\) (la différence entre les deux résultats est due aux erreurs de lecture graphique).

point \(E\) : a pour abscisse \(20\), donc \(f'(20) = 0\).