Exercices de probas

p 329 n° 80

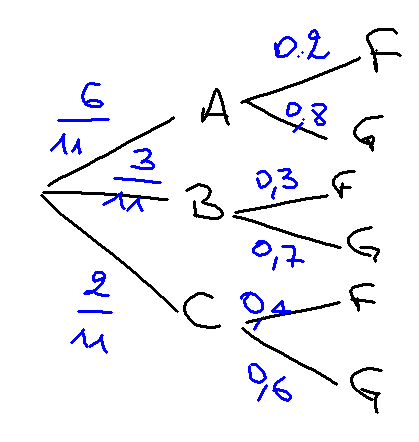
• p(A) est le double de \(p(B)\) donc \(p(A)=2 p(B)\), d'où \(p(B)= \dfrac{p}{2}\)
• p(A) est le triple de \(p(C)\) donc \(p(A)=3p(C)\), d'où \(p(C)= \dfrac{p}{3}\)

La somme des probas des branches issues d'un même noeud vaut \(1\) :

• \(p + \dfrac{1}{2}p + \dfrac{1}{3}p = 1\)
• \(\dfrac{6p}{6} + \dfrac{3p}{6} + \dfrac{2p}{6} = \dfrac{6}{6}\)
• \(p = \dfrac{6}{11}\)

arbre de probas n° 80

probabilité que l'étudiant soit un garçon :

• \(P(G) = P(A \cap G) + P(B \cap G) + P(C \cap G)\)
• \(P(G) = P(A) \times P_A(G) + P(B) \times P_B(G) + P(C) \times P_C(G)\)
• \(P(G) = \dfrac{6}{11} \times 0,8 + \dfrac{3}{11} \times 0,7 + \dfrac{2}{11} \times 0,6\)
• \(P(G) = \dfrac{81}{110}\)

Proba d'être dans la filière A, sachant que c'est un garçon :

\(P_G(A) = \dfrac{P(A \cap G)}{P(G)} = \dfrac{\frac{48}{110}}{\frac{81}{110}} = \dfrac{48}{81} = \dfrac{16}{27}\)

Proba d'être dans la filière B, sachant que c'est une fille :

\(P_F(B) = \dfrac{P(F \cap B)}{P(F)}\)

Or \(F\) et \(G\) sont des événements contraires, donc \(P(F) = 1 - P(G)\)

\(P_F(B)= \dfrac{\frac{3}{11} \times 0,3}{1 - \frac{81}{110}} = \dfrac{9}{29}\)

p 329 n° 89

• événement A : "le jeton est rouge"
• événement B : "le jeton porte le n° 0"

1. nb de jetons dans le sac

il y a 100 jetons rouges + 30 jetons verts avec n° 0 + \(n\) jetons verts avec n° 1 ; donc (130 + n) jetons en tout.

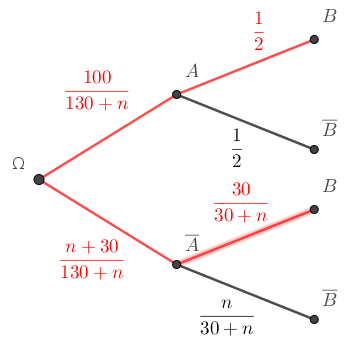
2. Pour la suite, on peut travailler sur l'arbre suivant qui traduit l'énoncé.

arbre de probas n° 89

1. \(P_A(B) = \dfrac{1}{2}\)

2. \(P(B) = P(A \cap B) + P(\bar{A} \cap B)\) \(P(B) = P(A) \times P_A(B) + P(\bar{A}) \times P_{\bar{A}}(B)\) \(P(B) = \dfrac{100}{130 + n} \times \dfrac{1}{2} + \dfrac{n + 30}{130 + n} \times \dfrac{30}{30 + n}\) \(P(B) = \dfrac{80}{130 + n}\)

3. les événements A et B sont indépendants si \(P(B) = P_A(B)\)

   on cherche \(n\) tel que \(\dfrac{80}{130 + n} = \dfrac12\) \(n=30\)

   Les événements A et B sont indépendants si le sac contient 100 jetons rouges (50 portants le n° 0 et 50 portants le n° 1) et 60 jetons verts (30 portants le n° 0 et 30 portants le n° 1).

p 333 n° 100

Le plus simple est de raisonner sur la tableau suivant qui modélise la situation

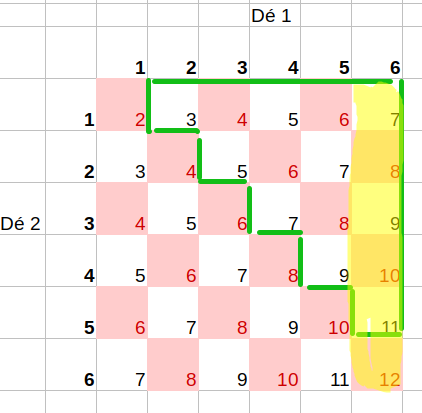
tableau de probas n° 100

1. Calcul des probabilités :

Utiliser la formule : \(\dfrac{\text{nb. cas favorables}}{\text{nb. cas total}}\)

• \(P_A(B)\) : on se place dans l'univers A (les cases roses) et on compte le nombre de cases de la zone jaune :

\(P_A(B)= \dfrac{3}{18} = \dfrac16\)

• \(P_B(C)\) : on se place dans l'univers B (les cases jaunes) et on compte le nombre de cases de la zone verte :

\(P_B(C) = \dfrac56\)

• \(P_A(C)\) : on se place dans l'univers A (les cases roses) et on compte le nombre de cases de la zone verte :

\(P_A(C) = \dfrac{6}{18} = \dfrac13\)

2. Indépendance de A et B ssi \(P(B) = P_A(B)\)

\(P(B) = \dfrac{6}{36} = \dfrac16 = P_A(B)\) : donc les événements sont indépendants.

3. Indépendance de A et C ssi \(P(C) = P_A(C)\)

\(P(C) = \dfrac{15}{36} \neq P_A(C)\) : les événements ne sont pas indépendants.

4. Indépendance de B et C ssi \(P(C) = P_B(C)\)

\(P(C) = \dfrac{15}{36} \neq P_B(C)\) : les événements ne sont pas indépendants.