p 57 n° 77

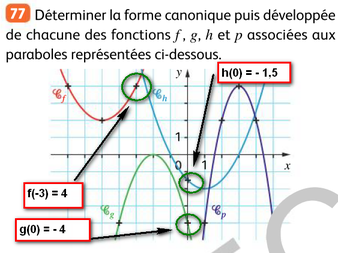
fonction \(f\)

orientée vers "le haut", donc \(a > 0\)
sommet \((-5\,; 2)\) donc \(f(x) = a(x - (-5))^2 + 2\)
on lit \(f(-3) = 4\) donc \(f(-3) = a(-3 + 5)^2 + 2 \Leftrightarrow 4= a(-3 + 5)^2 + 2 \Leftrightarrow a = \dfrac{2}{4} = \dfrac{1}{2}\)
donc \(f(x) = \dfrac{1}{2} (x + 5)^2 + 2\)

de la forme \(a(x - \alpha)^2\) (tangente à l'axe des abscisses = id. remarquable)

\(g(x) = a(x + 2)^2\)

on sait \(g(0) = -4\) donc \(a = -1\)

c'est à dire \(g(x)= -(x + 2)^2\).

\(h(x) = a(x-x_1)(x - x_2)\)

on lit \(x_1= -1\) et \(x_2 = 3\),

on remarque que \(h(0) = -1,5\),

donc \(\dots\) \(h(x) = \dfrac12(x + 1)(x -3)\)

\(p(x) = -2(x - 3)^2 + 4\)

longueur de la ficelle = 1 unité. expérience : \(x = 0,m\) (pour novembre on a \(x = 0,11\))

pour le carré : côté vaut \(\dfrac{0,11}{4}\)

donc \(\mathscr A_c = \dfrac{0,11}{4} \times \dfrac{0,11}{4} = \dfrac{0,0121}{16} \approx 0,00075\)
pour le rectangle : \(p = 2 \times (\ell + L) = 0,89\)

or \(L = 2 \times \ell\)

donc \(2 \times (\ell + 2 \ell) = 0,89 \Leftrightarrow \ell = \dfrac{0,89}{6} \approx 0,148\)

donc \(\mathscr A_r = L \times \ell = 2 \ell \times \ell = 2 \ell^2\) \(\mathscr A_r = 2 \times \left(\dfrac{0,89}{6}\right)^2 \approx 0,044\)
somme des aires est à peu près égale à \(0,00075 + 0,044 = 0,04475\)

remarque : 1 m = 100 cm, donc \(1 m^2 = 10000 cm^2\)

pour le carré : côté vaut \(\dfrac{x}{4}\) donc \(\mathscr A_c = \dfrac{x}{4} \times \dfrac{x}{4} = \dfrac{x^2}{16}\)
pour le rectangle : \(p = 2 \times (\ell + L) = 1 - x\) or \(L = 2 \times \ell\) donc \(2 \times (\ell + 2 \ell) = 1 - x \Leftrightarrow \ell = \dfrac{1-x}{6}\) donc \(\mathscr A_r = L \times \ell = 2 \ell \times \ell = 2 \ell^2\) \(\mathscr A_r = 2 \times \left(\dfrac{1-x}{6}\right)^2\)