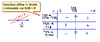
p 141 n° 1
question 5 : on cherche \(n\) tel que \(u_n > 1,91\) quand la suite est définie de façon explicite : on résous l'inéquation. on cherche \(n\) tel que \(\dfrac{2n}{n+2} > 1,91\)
prudent : \(\dfrac{2n}{n+2} - 1,91 > 0\) \(\Leftrightarrow \dfrac{2n}{n+2} - \dfrac{1,91 \times (n+2)}{n + 2} > 0\) \(\Leftrightarrow \dfrac{0,09 n - 3,82}{n+2} > 0\)
\(\Leftrightarrow n > \dfrac{382}{9} \approx 42,4\)
astuce : \( n \in \mathbb{N}\) donc \(n + 2 > 0\) donc on peut écrire : \(\dfrac{2n}{n+2} \times (n+2)> 1,91 \times (n+2)\) \(\Leftrightarrow 2n > 1,91 (n+ 2)\) \(\Leftrightarrow 0,09 n > 3,82\)
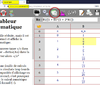
p 141 n ° 2
utilisation du tableur (calculatrice, xcas www.xcasenligne.fr avec FireFox)
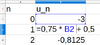
on lit que pour \(n \geqslant 14\) : \(u_n > 1,91\).
p. 160 n° 84
conjecture : tous les termes sont de la forme "\(1\) sur quelque chose"