p. 162 n° 95

\(\begin{cases} u_0 = 3 \\ u_{n+1} = \dfrac{1 - u_n}{1+ u_n} \end{cases}\)

1. représentation à l'aide de la calculatrice.

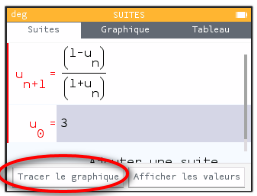
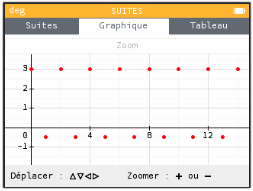
La suite n'est pas monotonne : il semble que les termes de rang pair valent tous \(3\) et que ceux de rang impair valent tous \(-\frac12\).

2. expression de \(u_{n+2}\) en fonction de \(u_n\).

\(u_{n+2} = \dfrac{1 - u_{n+1}}{1 + u_{n+1}}\)

or \(u_{n+1} = \dfrac{1 - u_n}{1 + u_n}\)

d'où : \(u_{n+2} = \dfrac{1 - \frac{1 - u_n}{1 + u_n}}{1 + \frac{1 - u_n}{1 + u_n}}\)

\(u_{n+2} = \dfrac{1 + u_n - (1 - u_n)}{1 + u_n + (1 + u_n)} = u_n\)

Conclusion :

• si \(n\) est pair : \(u_n = u_0 = 3\)
• si \(n\) est impair : \(u_{n+1} = u_1 = \dfrac{1 - u_0}{1 + u_0} = -\dfrac12\)

p 162 n° 94

\(\begin{cases} u_0 = 3 \\ u_{n+1} = 2u_n - 4 \end{cases}\)

1. Calculatrice

Conjecture : la suite est décroissante (et diverge vers \(-\infty\))

2. Suite \((v_n)\).

Remarque : pour tout \(n \in \mathbb{N} : v_n = u_{n+1} - u_n\).

donc \(v_n = 2 u_n -4 - u_n = u_n - 4\)

2.a \(v_{n+1} = u_{n+1} - 4 = 2 u_n - 4 - 4 = 2 (u_n - 4) = 2 v_n\).

C'est à dire que chaque terme est le double du précédent.

2.b \(v_0 = u_0 - 4 = 3 - 4 = -1\).

Comme on double à chaque fois, quelque soit \(n \in \mathbb{N} : v_n < 0\)

2.c sens de variation de \((u_n)\).

On étudie le signe de la différence de deux termes consécutifs :

\(u_{n+1} - u_n = v_n < 0\), donc la suite \((u_n)\) est décroissante.

3. différentes valeurs de \(u_0\).

• si \(u_0 = 6\), alors \(v_0 = 6 - 4 = 2\),

donc pour tout \(n \in \mathbb{N} : v_n > 0\)

et \(u_{n+1} - u_n = v_n > 0\), donc la suite \((u_n)\) est croissante.

• si \(u_0 = 4\), alors \(v_0 = 4 - 4 = 0\),

donc pour tout \(n \in \mathbb{N} : v_n = 0\)

et \(u_{n+1} - u_n = v_n = 0\), donc la suite \((u_n)\) est constante.