p 69 B

lecture de coefficients directeurs équation réduite : $y = mx + p$

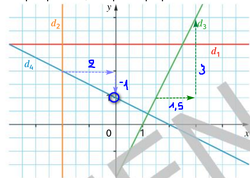
$d_1 : y = 3$ , c'est une droite parallèle à l'axe des abscisses, son coefficient directeur est nul.

$d_2$ est une droite parallèle à l'axe des ordonnées : ce n'est pas une fonction ! mais cette droite a une équation : $x=-2$.

$d_3$ : par lecture graphique $m_3 = \dfrac{3}{1,5} = 2$

$d_4$ : la droite "descend", donc le coefficient directeur est négatif (il vaut $-0,5$) L'équation est de la forme $y=mx+ p$, avec $p$ qui est "l'ordonnée à l'origine". Ici $p= 1$, donc $d_4$ a pour équation $y=-0,5 x + 1$

p.83 n° 16

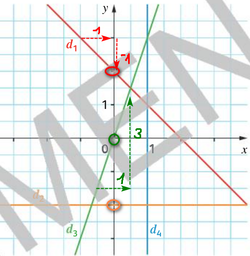
$d_1$ : $m_1 = \dfrac{\Delta_y}{\Delta_x} = \dfrac{-1}{1} = -1$ et $p_1 = 2$ d'où l'équation : $y = -x + 2$

$d_2$ : est parallèle à l'axe des abscisses donc $m_2 = 0$ et $p_2 = -2$ d'où l'équation : $y = -2$

$d_3$ : $m_3 = \dfrac{\Delta_y}{\Delta_x} = \dfrac{3}{1} = 3$ et $p_3 = 0$ d'où l'équation : $y = 3x $ (c'est une fonction linéaire)

$d_4$ ne représente pas une fonction, donc pas d'équation réduite !