p 83 n° 18
équation réduite de droite : \(y= mx + p\)
droite \(d_1\)
\(m = 2\) et \(A(-2\,; 4)\)
proposition : \(y = 2x + \dfrac{17}{2}\)
vérifications possibles :
- représentation graphique + lecture de l'ordonnée à l'origine
- remplacer \(x\) par l'abscisse de \(A\) (dans l''équation) et vérifier que le calcul donne l'ordonnée de \(A\).
Rappels :
- une droite est portée par un vecteur directeur qui a pour coordonnées \((1\,; m)\) (\(m\) étant le coefficient directeur de la droite).
- la direction d'un vecteur représente son "inclinaison" par rapport à l'axe des abscisses.
- la transformation liée aux vecteurs est la translation.
Conclusion : l'équation de la droite n'est pas : \(y = 2x + \dfrac{17}{2}\)
Méthode possible : à partir \(y=mx +p\), sachant que \(m=2\), remplacer \(y\) par \({\color{red}{y_A}}\) et \(x\) par \({\color{blue}{x_A}}\)
\({\color{red}4} = 2 \times {\color{blue}{(-2)}} + p \Leftrightarrow p=8\)
on trouve \(y = 2x + 8\)
de même :
- \(d_2 : y = - \dfrac12 x + \dfrac72\)
- \(d_3 : y = \dfrac13\)
remarque sur les équations de droite
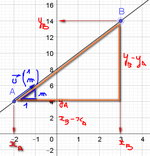
Triangle orange et triangle bleu = théorème de Thalès.
\({\color{orange}{\dfrac{y_B-y_A}{x_B-x_A}}} = {\color{blue}{\dfrac{m}{1}}}\)
\(y_B -y_A = m (x_B - x_A)\)
\(y_B = m (x_B - x_A) + y_A\)
Dans le cas général, si \(A\) est connu on note ses coordonnées \((x_A\,; y_A)\) et si \(B\) n'est pas connu, on note ses coordonnées \((x\,;y)\) dans cas l'équation s'écrit :
\(y = m (x - x_A) + y_A\)
Dans le cas particulier d'une tangente à la courbe.
l'équation de la tangente à la courbe représentative de la fonction \(f\), au point \(A\) d'abscisse \(a\) et d'ordonnée \(f(a)\) s'écrit :
\(y = f'(a) (x - a) + f(a)\)
avec \(f'(a)\) le coefficient directeur de la tangente.
p 73. n° 1
\(f(x)= -2x^2 + 5\)
\(\tau(h) = \dfrac{f(a +h) - f(a)}{h}\)
1.a pour \(a = 4\) \(\tau(h) = \dfrac{{\color{red}{f(4 +h)}} - {\color{blue}{f(4)}}}{h}\)
\(\tau(h) = \dfrac{{\color{red}{-2(4 +h)^2 + 5}} - ({\color{blue}{-2 \times 4^2 + 5}})}{h}\)
\(\tau(h) = \dfrac{{\color{red}{-2(4^2 + 8h + h^2) + 5}} - ({\color{blue}{-2 \times 4^2 + 5}})}{h}\)
\(\tau(h) = \dfrac{{\color{red}{-2 \times 4^2 - 16 h -2 h^2 + 5}} + {\color{blue}{2 \times 4^2 - 5}}}{h}\)
\(\tau(h) = \dfrac{- 16 h -2 h^2 }{h} = \dfrac{- 16 h}{h} - \dfrac{2 h^2 }{h} = -16 - 2h\)
ou bien : \(\tau(h) = \dfrac{- 16 h -2 h^2 }{h} = \dfrac{h(- 16 - 2 h)}{h} = -16 - 2h\)
donc \(\lim\limits_{h \to 0} \tau(h) = \lim\limits_{h \to 0} -16 - 2h = -16\)
le nombre dérivé de \(f\) en \(a=4\) est \(f'(4)\) et il vaut \(-16\), d'où \(f'(4) = -16\).
Bonus : l'équation de la tangente à \(\mathscr C_f\) au point d'abscisse \(4\) est :
\(y = f'(a)(x-a) + f(a)\) donc \(y = f'(4)(x-4) + f(4)\)
\(y = -16(x - 4) + (-27) = -16x + 37\)