Problème des tangentes à la parabole.
On avait trouvé : \(x_M = \dfrac{x_A + x_B}{2}\) Il fallait trouver l'expression de \(y_M\) à l'aide de \(y_M =2x_A x_M - x_A^2\)
On trouve : \(y_M = x_A \times x_B\).
p 90 n° 74
la droite d'équation \(y=-2x+3\) est tangente à la courbe au point \(A\) d'abscisse \(3\).
On peut représenter la situation : pas le choix pour tracer la tangente, on suppose une courbe possible :
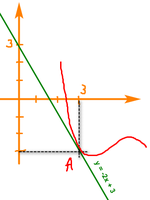
Pour \(x=3\), on trouve \(y=-2 \times 3 + 3 = -3\) donc le point \(A\) a pour coordonnées \((3\,; -3)\) (il appartient à la courbe et à la tangente).
p 90 n° 72
On peut dessiner la tangente en \(a =0\). Question, la tangente est-elle la représentation d'une fonction affine ? Si oui, la fonction est dérivable en \(0\), sinon, elle ne l'est pas...
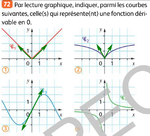
- la tangente est "cassée" en \(0\), donc la fonction n'est pas dérivable en \(0\).
Ou bien : la tangente à gauche de \(0\), pour des valeurs de \(x\) négatives, a pour coefficient directeur \(-1\) ; la tangente à droite de \(0\), pour des valeurs de \(x\) positives, a pour coefficient directeur \(1\) ; comme \(-1 \neq 1\), la fonction n'est pas dérivable en \(0\).
même idée que (1) : la fonction n'est pas dérivable en \(0\).
la tangente représente une fonction affine : la fonction est dérivable en \(0\).
On reconnaît la fonction inverse : elle n'est pas définie en \(0\), donc elle ne peut pas être dérivable en \(0\).
p 93 n° 92
équation de la tangente : \(y= f'(a)(x - a) + f(a)\)
Pour la fonction carrée, la tangente au point d'abscisse \(a\) est donnée par : \(y = 2a (x- a) + a^2 = 2ax - a^2\)
Pour la fonction inverse, la tangente au point d'abscisse \(b\) est donnée par : \(y = \dfrac{-1}{b^2} (x - b) + \dfrac{1}{b} = \dfrac{-1}{b^2} x + \dfrac{2}{b}\)
Les tangentes sont confondues si elles ont la même équation.
même coefficient directeur, il faut : \(2a = \dfrac{-1}{b^2}\)
même ordonnée à l'origine, il faut : \(-a^2 = \dfrac{2}{b}\)
\(\begin{cases} 2a &= \dfrac{-1}{b^2} \\ -a^2 &= \dfrac{2}{b} \end{cases} \Leftrightarrow \begin{cases} a &= \dfrac{-1}{2b^2} \\ -\left(\dfrac{-1}{2b^2}\right)^2 &= \dfrac{2}{b} \end{cases} \Leftrightarrow \begin{cases} a &= \dfrac{-1}{2b^2} \\ -\dfrac{1}{4b^4} &= \dfrac{2}{b} \end{cases} \Leftrightarrow \begin{cases} a &= \dfrac{-1}{2b^2} \\ -1 &= 8 b^3 \end{cases} \Leftrightarrow \begin{cases} a &= \dfrac{-1}{2b^2} \\ -1 &= (2 b)^3 (*) \end{cases} \Leftrightarrow \begin{cases} a &= \dfrac{-1}{2b^2} \\ b &= -\dfrac{1}{2} \end{cases} \Leftrightarrow \begin{cases} a &= -2 \\ b &= -\dfrac{1}{2} \end{cases}\)
(*) ici il faut expliquer... la fonction cube est strictement croissante et le seul antécédent de \((-1)\) est \((-1)\) (en effet \((-1)^3= -1\)), donc il faut \(2b = -1 \Leftrightarrow b = - \dfrac{1}{2}\).
Conclusion : la tangente à la parabole au point d'abscisse \((-2)\) est aussi tangente à l'hyperbole au point d'abscisse \(-\dfrac12\).