p 147 n° 9

suite arithmétique est de la forme : \( u_{n+1} - u_n = r \)

la différence entre deux termes consécutifs est constante.

Or \( u_{n+1} - u_n = r \Leftrightarrow u_{n+1} = u_n + r\)

a)

• suite arithmétique de raison \(r=10\)
• On ne peut pas calculer les premiers termes car il manque \(u_0\)

b)

• ce n'est pas une suite arithmétique car \(\color{red}{2} u_n + 4\) : le coefficient de \(u_n\) doit être 1.
• On ne peut pas calculer les premiers termes car il manque \(u_0\)

c)

• forme explicite : \(u_n = n \times r + u_0\)
• ici \(u_n = n^{\color{red}{2}}\), ce qui ne correspond pas à la définition.
• On ne calculer les premiers termes : \(u_0 = 0^2 = 0\) ; \(u_1 = 1^2 = 1\) ; \(u_2 = 2^2 = 4\).

d) : suite artihmétique de raison \(r= - 1\) (forme par récurrence); on ne peut pas calculer les premiers termes : il manque \(u_0\).

e) : suite arithmétique

• définition explicite : \(u_n = u_0 + n \times r = r \times n + u_0 \)
• ici : \(r = 3 \) et \(u_0 = -5 \).
• \(u_0 = -5\) ; \(u_1 = 3 \times 1 - 5 = -2\) ; \(u_2 = 3 \times 2 - 5 = 1\).

f) non arithmétique (voir b)

p 158 n° 59

1.) On sait que la suite est arithmétique, on connaît \(u_0\) et \(r\), donc on utilise la forme explicite : \(u_n = u_0 + nr = -1 + n \times 4 = 4n - 1\)

donc \(u_5 = 4 \times 5 - 1 = 19\) et \(u_{10} =4 \times 10 - 1 = 39\)

2.) Par défintion : \(u_n = u_0 + n \times \dfrac{1}{3}\)

\(u_{\color{red}{12}} = 9 \Leftrightarrow u_0 + \color{red}{12}\times \dfrac{1}{3} = 9 \Leftrightarrow u_0 + 4 = 9 \Leftrightarrow u_0 = 5 \)

donc \(u_n = 5 + n \times \dfrac{1}{3}\)

donc \(u_6 = 5 + 6 \times \dfrac{1}{3} = 7\)

3.) Par défintion : \(u_n = 1 + n \times r\)

\(u_{\color{red}{10}} = 31 \Leftrightarrow 1 + \color{red}{10} \times r = 31 \Leftrightarrow 1 + 10 r = 31 \Leftrightarrow r= 3\)

donc \(u_n = 1 + n \times 3 = 1 + 3n\)

donc \(u_{2\,018} = 1 + 3 \times 2\,018 = 6\,055\)

4.) Par défintion : \(u_n = 1 + n \times r\)

donc \(u_5 = u_0 + 5r = -12\) et \(u_{13} = u_0 + 13r = -44\)

il faut résoudre le système : \(\left\lbrace \begin{array}{l} u_0 + 5r = -12 \\ u_0 + 13r = -44 \end{array}\right.\)

.... résolution du système ....

ici : astuce. La suite est arithmétique, image mentale de l'escalier !

de \(u_5\) à \(u_{13}\) il y a \(13 - 5 = 8\) marches, donc \(\color{blue}{u_5} + 8r = \color{green}{u_{13}}\)

il suffit de résoudre \(\color{blue}{-12} + 8r = \color{green}{-44} \Leftrightarrow r= -4\)

On sait que \(u_0 + 5r = -12 \Leftrightarrow u_0 + 5 \times (-4) = -12 \Leftrightarrow u_0 = 8 \)

Donc \(u_n = 8 - 4n \)

p 158 n°63

1.) \(S_1 = 1 + 2 + 3 + \ldots + 100\)

Somme des n premiers entiers : \( S_1 = \dfrac{n(n+1)}{2}\) avec \(n = 500\), donc \(S_1 = \dfrac{500 \times (500 + 1)}{2} = 125\,250 \)

2.) \(S_2 = 2 + 4 + 6 + \ldots + 200\)

Posons \(u_n = 2 + 2n\) ; on a donc

• \(u_0 = 2 + 2 \times 0 = 2\)
• \(u_1 = 2 + 2 \times 1 = 4\)
• \(u_2 = 2 + 2 \times 2 = 6\)
• ...
• \(u_{99} = 2 + 2 \times 99 = 200\)

Donc \(S_2 = u_0 + u_1 + u_2 + \ldots + u_{99} = (99 + 1) \dfrac{u_0 + u_n}{2} = 100 \times \dfrac{2 + 200}{2}= 10\,100\)

3.) \(S_3 = 50 + 51 + 52 +\ldots + 100\)

Posons \(u_n = 50 + n\) ; on a donc

• \(u_0 = 50 + 0 = 50\)
• \(u_1 = 50 + 1 = 51\)
• \(u_2 = 50 + 2 = 52\)
• ...
• \(u_{50} = 50 + 50 = 100\)

Donc \(S_3 = u_0 + u_1 + u_2 + \ldots + u_{50} = (50 + 1) \dfrac{u_0 + u_n}{2} = 51 \times \dfrac{50 + 100}{2}= 3\,825\)

4.) \(S_4 = 4 + 7 + 10 +\ldots + 91\)

Posons \(u_n = 4 + 3n\) ; on a donc

• \(u_0 = 4 + 3 \times 0 = 4\)
• \(u_1 = 4 + 3 \times 1 = 7\)
• \(u_2 = 4 + 3 \times 2 = 10\)
• ...
• \(u_{29} = 4 + 3 \times 29 = 91\)

Donc \(S_4 = u_0 + u_1 + u_2 + \ldots + u_{29} = (29 + 1) \dfrac{u_0 + u_n}{2} = 30 \times \dfrac{4 + 91}{2}= 1\,425\)

p. 163 n° 108

\(u_n = \dfrac{3n^2 + 16n +5}{n+ 5}\)

calcul des premiers termes :

• \(u_0 = \dfrac{3 \times 0^2 + 16 \times 0 +5}{0 + 5} = 1\)
• \(u_1 = \dfrac{3 \times 1^2 + 16 \times 1 +5}{1 + 5} = 4\)
• \(u_2 = \dfrac{3 \times 2^2 + 16 \times 2 +5}{2 + 5} = 7\)

Conjecture : \((u_n)\) est une suite arithmétique de premier terme \(u_0 = 1\) et de raison 3 ; son expression est \(u_n = 1 + 3n\). Et donc la suite serait croissante.

on montre que \(3n^2 + 16 n + 5 = (3n +1)(n+ 5)\)

donc \(u_n = \dfrac{(3n+1)(n+5)}{n+5} = 3n + 1\)

la conjecture est vérifiée.

p. 149 n° 11

• \(u_{n+1}= 5 u_n\) : définition par récurrence d'une suite géométrique de raison 5, mais on ne connaît pas \(u_0\) : cela ne définit pas une suite géométrique.
• \(u_n = 5n\) : défintion explicite d'une suite arithmétique.
• \(u_n = 5^n \) : défintion explicite d'une suite géométrique de raison 5.
• \(u_n = 2 \color{red}{+} 3^n\) : ce n'est pas une suite géométrique.
• \(u_n = 2 \color{red}{\times} 3^n\)... est une suite géométrique de raison 3.
• \(u_{n+1} = 2 u_{n-1} + 3\) : ce n'est pas une suite géométrique.

p.164 n° 117

Dans cette exercice, on sait que \((u_n)\) est une suite géométrique, donc on peut utiliser une des deux définitions :

• explicite : \(u_n = u_0 \times q^n\)
• par récurrence : \(\left\lbrace\begin{array}{l} u_0= a \\ u_{n+1} = q \times u_n \\ \end{array}\right.\)

\(u_3= 4\) et \(u_{10}=312\,500\)

\(u_3 = 4\), donc \(u_0 \times q^3 = 4\)

\(u_{10} = 312\,500\), donc \(u_0 \times q^{10} = 312\,500\)

astuce de caclul : les puissances copmliquant le calcul, on travail sur le quotient \(\dfrac{u_{10}}{u_3}\)

\(\dfrac{u_{10}}{u_3} = \dfrac{312\,500}{4} = 78\,125\)

mais \(\dfrac{u_{10}}{u_3} = \dfrac{u_0 \times q^{10}}{u_0 \times q^3} = q^{10 - 3} = q^7\)

il faut donc trouver un nombre q tel que \(q^7 = 78\,125\)... On tente \(q = 5\) car une puissance de 5 a toujours 5 comme chiffre des unités.

\( 5^7 = 78\,125\).. yes !, donc \(q = 5\).

on cherche \(u_0\), sachant que \(u_3 = u_0 \times q^3 = 4\)

donc \(u_0 \times 5^3 = 4 \Leftrightarrow u_0 = \dfrac{4}{5^3} \Leftrightarrow u_0 = \dfrac{4}{125}\)

donc la suite est : \(u_n = \dfrac{4}{125} \times 5^n\)

\(u_2 = \dfrac{5}{9}\) et \(u_7= - \dfrac{5}{2\,187}\)

même technique de calcul...

\( \dfrac{u_7}{u_2} = \dfrac{-\dfrac{5}{2\,187}}{\dfrac{5}{9}} = \dfrac{5}{-2\,187} \times \dfrac{9}{5} = \dfrac{1}{- 243}\)

diviser, c'est multiplier par l'inverse.

\( \dfrac{u_7}{u_2} = \dfrac{u_0 \times q^7}{u_0 \times q^2} = q^5\)

donc on cherche \(q\) tel que \(q^5 = -\dfrac{1}{243}\). On remarque que 243 est un multiple de 3 (la somme des chiffres vaut 6), donc on suppose que \(q = -\dfrac{1}{3}\)...

\(\left(-\dfrac{1}{3}\right)^5 = -\dfrac{1}{243} \)... yes (deuxième fois).

donc \(u_n = u_0 \times \left(-\dfrac{1}{3}\right)^n\)

on sait que

• \(u_2 = u_0 \times q^2 = u_0 \times \left(-\dfrac{1}{3}\right)^2 = u_0 \times \dfrac{1}{9}\)
• et que \(u_2 = \dfrac{5}{9}\)

On en déduit que \(u_0 = 5\) et que \(u_n = 5 \times \left(-\dfrac13\right)^n\)

\(u_2 = 2\) et \(u_6 = 32\) et \(q > 0\)

\(u_2 = u_0 \times q^2 = 2\)

\(u_6 = u_0 \times q^6 = 32\)

donc \(\dfrac{u_6}{u_2} = \dfrac{u_0 \times q^2}{u_0 \times q^6} = q^4\)

et \(\dfrac{u_6}{u_2} = \dfrac{32}{2} = 16\)

On cherche \(q\) tel que \(q^4 = 16\) : deux possibilités \(q=-2\) ou \(q = 2\) or \(q > 0\), donc \(q=2\).

d'où \(u_n = u_0 \times 2^n\) ; or \(u_2 = 2 = u_0 \times 2^2 \Leftrightarrow u_0 = \dfrac{1}{2}\)

donc \(u_n = \dfrac12 \times 2^n = 2^{n-1}\)

\(u_4 = \dfrac{15}{8}\) et \(u_{10} = \dfrac{15}{512}\) et \(q<0\)

même raisonnement : \(q^6 = \dfrac1{64}\) or \(64 = 2^6 = (-2)^6\)

comme \(q<0\), on en déduit que \(q=-\dfrac12\)

donc \(u_n = u_0 \times \left(-\dfrac12\right)^n\)

puis \(u_n = 30 \times \left(-\dfrac12\right)^n \)

p. 165 n° 119

somme \(S_1\)

on remarque que

• \(64 = 32 \times 2\)
• \(128 = 64 \times 2\)

donc la suite est définie par \(u_{n+1} = 2 \times u_n\), donc la raison est \(q=2\) et le premier terme est \(u_0 = 32\)

On en déduit que \(\color{red}{u_n} = u_0 \times q^n = \color{red}{32 \times 2^n}\)

On veut calculer \(S = u_0 + u_1 + u_2 + \ldots + u_n = \color{blue}{u_0 \times \dfrac{1 - q^{n+1}}{1-q}}\)

On cherche la valeur de \(n\) sachant que \(u_n = 131\,072 = \color{red}{32 \times 2^n}\)

\(\Leftrightarrow 4\,096 = 2^n\)

On sait que \(2^{10} = 1\,024\)

donc \(4\,096 = 1\,024 \times 2 \times 2 = 2^{10} \times 2^2 = 2^{12}\)

donc \(n=12\) ; d'où \(S = \color{blue}{u_0 \times \dfrac{1 - q^{n+1}}{1-q}} = 32 \times \dfrac{1 - 2^{12 + 1}}{1 -2} = 262\,112\)

somme \(S_2\)

somme \(S_3\)

on remarque que

• \(5 = 3 \times \dfrac{5}{3}\)
• \(\dfrac{25}{3} = 5 \times \dfrac{5}{3}\)

donc la suite est définie par \(u_{n+1} = \dfrac{5}{3} \times u_n\), donc la raison est \(q=\dfrac{5}{3}\) et le premier terme est \(u_0 = 3\)

On en déduit que \(\color{red}{u_n} = u_0 \times q^n = \color{red}{3 \times \left(\dfrac{5}{3}\right)^n}\)

On veut calculer \(S = u_0 + u_1 + u_2 + \ldots + u_n = \color{blue}{u_0 \times \dfrac{1 - q^{n+1}}{1-q}}\)

On cherche la valeur de \(n\) sachant que \(u_n = \dfrac{390\,625}{2\,187} = \color{red}{3 \times \left(\dfrac{5}{3}\right)^n}\)

\(\Leftrightarrow \dfrac{390\,625}{2\,187} \times \dfrac{1}{3} = \dfrac{390\,625}{6\,561} = \left(\dfrac{5}{3}\right)^n\)

En travaillant par essai-erreur : \(\left(\dfrac{5}{3}\right)^8 = \dfrac{390\,625}{6\,561}\)

donc \(n=8\) ; d'où \(S = \color{blue}{u_0 \times \dfrac{1 - q^{n+1}}{1-q}} = 3 \times \dfrac{1 - \left(\frac{5}{3}\right)^{8 + 1}}{1 -\frac{5}{3}} = \dfrac{966\,721}{2\,187}\)

p. 166 n° 128

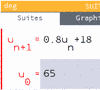
Calcul des premiers termes

On remarque que :

• \(u_1 - u_0 \neq u_2 - u_1 \) donc la suite ne peut pas être artihmétique ;
• \( u_1 = \dfrac{70}{65} u_0\) et \(u_2 = \dfrac{74}{70} u_1\) et \( \dfrac{70}{65} \neq \dfrac{74}{70}\) : donc la suite ne peut pas être géométrique.

suite \((v_n)\)

posons : \( \color{purple}{v_n = u_n -90} \)

donc \( v_{n + 1} = \color{blue}{u_{n+1}} - 90 \)

\( \Leftrightarrow v_{n + 1} = \color{blue}{0,8 u_{n} + 18} - 90 \)

\( \Leftrightarrow v_{n + 1} = 0,8 u_{n} - 72 \)

\( \Leftrightarrow v_{n + 1} = 0,8 (u_{n} - 90) \)

\( \Leftrightarrow v_{n + 1} = 0,8 (\color{purple}{u_{n} - 90}) \)

\( \Leftrightarrow v_{n + 1} = 0,8 (\color{purple}{v_{n}}) \)

donc la suite \((v_n)\) est géométrique de raison 0,8 et de premier terme \(v_0 = u_0 - 90 = -25\)