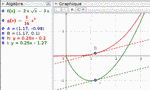
p 122 n° 77
Recherche et conjecture.
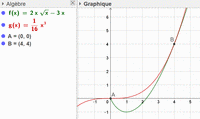lecture graphique : les courbes se coupent en \(A(0\,; 0)\) et \(B(4\,; 4)\)
Si un point appartient à une courbe, ses coordonnées doivent vérifier l'équation de la fonction.
- pour le point \(A\) :
- \(f(0) = 2 \times 0 \times \sqrt{0} - 3 \times 0 = 0\) : le point \(A(0\,;0)\) appartient à \(\mathscr{C}_f\).
- \(g(0) = \dfrac{1}{16} \times 0^3 = 0\) : le point \(A(0\,;0)\) appartient à \(\mathscr{C}_g\).
- donc les courbes sont sécantes en \(A\).
- pour le point \(B\):
- \(f(4) = 2 \times 4 \times \sqrt{4} - 3 \times 4 = 4\) : le point \(B(4\,;4)\) appartient à \(\mathscr{C}_f\).
- \(g(4) = \dfrac{1}{16}\times 4^3 = 4\) : le point \(B(4\,; 4)\) appartient à \(\mathscr{C}_g\).
- donc les courbes sont sécantes en \(B\).
normalement, il a aurait fallu résoudre \(f(x) = g(x)\) pour être certain qu'il n'y a que deux solutions.
C'est à dire résoudre :
\(2x \sqrt{x} - 3 x = \dfrac{1}{16}x^3\) \(\Leftrightarrow x \left( 32 \sqrt{x} - 48-x^2 \right) = 0\)
Mais ce n'est pas beau... Et on ne sait pas le faire actuellement !
Enfin... si pour les plus courageux : il suffit de poser \(X = \sqrt{x}\) puis de trouver les solutions de (je vous laisse comprendre pourquoi) \(-\dfrac{1}{16} X^4 + 2X -3 = 0\). Pour cela on remarque que \(X = 2\) est une racine évidente, donc on peut factoriser par \((X - 2)\) ; remarquer alors que \(X = 2\) est encore (!) une racine évidente, donc on peut de nouveau factoriser par \((X - 2)\) ; et on obtient \(-\dfrac{1}{16} X^4 + 2X -3 = 0 \Leftrightarrow -\dfrac{1}{16} (X - 2)^2 (X^2 + 4X + 12) \). Puis conclure en revenant à des solutions en \(x\)...
Tangente commune
Tangente commune : il faut le même coefficient directeur et (au choix) un point commun ou même ordonnée à l'origine.
le coefficient directeur de la tangente est le nombre dérivé.
dérivée de \(f\)
\(f(x) = \underbrace{2x \sqrt{x}}_{u(x)} - \underbrace{3x}_{v(x)}\) on a : \(u(x) = {\color{blue}{2x}} \times {\color{red}{\sqrt{x}}}\) (produit) donc \(u'(x) =2 \times \sqrt{x} + 2x \times \dfrac{1}{2\sqrt{x}} = 3\sqrt{x}\) (car \(\dfrac{x}{\sqrt{x}} = \dfrac{\sqrt{x} \times \sqrt{x}}{\sqrt{x}} = \sqrt{x}\))
donc \(f'(x) = 3\sqrt{x} - 3 = 3 \left(\sqrt{x} - 1\right)\)
dérivée de \(g\)
\(g(x) = \dfrac{1}{16}x^3\) donc \(g'(x) = \dfrac{1}{16} \times 3 x^2 = 3 \times \dfrac{1}{16} x^2\)
nombre dérivés égaux
on cherche \(x\) tel que \(f'(x) = g'(x)\)
\(\Leftrightarrow x^2 - 16\sqrt{x} + 16 = 0\) (je vous laisser chercher pourquoi.)
De même que précédemment, on ne sait pas résoudre cette équation, mais on peut vérifier que pour \(x=4\), elle est vérifiée.
Et cela suffit car il n'y a que deux points d'intersection : celui d'abscisse (\0\) et celui d'abscisse (\4\).
Donc \(f'(4) = g'(4)\) : les tangentes au point d'abscisse \(4\) sont donc parallèles, et comme elles passent par le point \(B\), elles sont confondues.
Pour les TRES courageux : une piste de travail pour chercher les abscisses des points qui ont le même nombre dérivé.
Poser
\(X = \sqrt{2}\) et remarquer que
\(X = 2\) est une solution de l'équation qui s'écrit donc :
\(-\dfrac{1}{16} (X-2) (X^3 +2X^2 + 4X - 8)=0\).
Ensuite grâce aux connaissances acquises à la fin de ce merveilleux chapitre, étudier les variations de
\(P(X) = X^3 +2X^2 + 4X - 8\)
et conclure... qu'on trouve une autre abscisse pour laquelle les tangentes ont le même coefficient directeur.
