• p 311 n° 6
• p 325 n° 69
• p 319 n° 43
• p 325 n° 78
• p 319 n° 48

p 311 n° 6

à l'aide du menu "stats" de la calculatrice

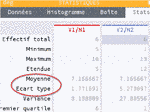
on trouve :

• série 1 : la moyenne (on la note \(\bar{x}\), et on lit "x barre") est \(\bar{x} \approx 7,17\) et l'écart-type (on le note \(\sigma\), et on lit "sigma") est \(\sigma \approx 1,8\)
• série 2 : \(\bar{x} \approx 7,17\) et \(\sigma \approx 5,3\)
• série 3 : \(\bar{x} \approx 13,17\) et \(\sigma \approx 1,8\)

pour vider les listes : NumWorks : dans le menu "Données", se mettre sur le titre de la colonne, puis bouton "OK"

p 325 n° 69

l'écart-type représente la dispertion autour de la moyenne : plus il petit, plus les valeurs seront groupées autour de la moyenne, et plus il est grand, plus les valeurs seront dispersées autour de la moyenne.

• graphique rouge : (5,5 ; 1,2)
• graphique vert : (5,5 ; 1,8)
• graphique bleu : (5,5 ; 3,05)

p 319 n° 43

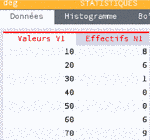
lecture du graphique : 8 individus ont la valeur 10 ; 20 individus ont la valeur 6 ...

moyenne pondérée :

\( \bar{x} = \dfrac{\text{somme des valeurs}~ \color{blue}{\text{affectées}}~ \color{red}{\text{des coefficients}}} {\text{somme des}~\color{red}{\text{coefficients}}}\)

\( \bar{x} = \dfrac{ 10 \color{blue}{\times} \color{red}{8} + 20 \color{blue}{\times} \color{red}{6} + 30 \color{blue}{\times} \color{red}{1} + 40 \color{blue}{\times} \color{red}{0} + 50 \color{blue}{\times} \color{red}{0} + 60 \color{blue}{\times} \color{red}{6} + 70 \color{blue}{\times} \color{red}{9} } {\color{red}{8} + \color{red}{6} + \color{red}{1} + \color{red}{0} + \color{red}{0} + \color{red}{6} + \color{red}{9} }\)

calculatrice : \(\bar{x} \approx 40,7 \) et \(\sigma \approx 26\)

l'intervalle \([\bar{x} - \sigma \,; \bar{x} + \sigma] = [40,6 - 26 \,; 40,6 + 26] = [14,6 \,; 66,6]\)

il y a \(N = 6+ 1 + 0 +0 + 6 = 13\) valeurs dans l'intervalle \([\bar{x} - \sigma \,; \bar{x} + \sigma]\)

la proportion des valeurs dans cet intervalle : \(p = \dfrac{13}{30} \approx 0,43\), donc environ 43% des valeurs appartiennt à l'intervalle \([\bar{x} - \sigma \,; \bar{x} + \sigma]\)

p 325 n° 78

il faut travailler avec le centre (moyenne des bornes inférieure et supérieure) de chaque classe (intervalle) : on lit 18 appartements d'une surface comprise entre 0 et 20 \(m^2\) exclus. Pour les calculs : on considère 18 appartements de 10 \(m^2\) (car \(\dfrac{0 + 20}{2} = 10\) ).

p 319 n° 48

exemple :

• évolution n° 1: +15 %
• évolution n° 2: -60 %
• évolution globale ?

\( p_0 \xrightarrow[\nearrow \,15\,\%]{} p_1 \xrightarrow[\searrow \,60\,\%]{} p_2\)

En cas de soucis, passer un calcul : poser \(p_0= 100\) :

\( 100 \xrightarrow[\nearrow \,15\,\%]{} 115 \xrightarrow{\times 0,4} 46\)

on sait que diminuer de 60 % c'est multiplier par \( \left( 1 - \dfrac{60}{100}\right) =0,4 \)

donc on passe de \( p_0 = 100 \) à \(p_2 = 46\) cela correspond à une baisse de 54 %

La méthode : utiliser les coefficients multiplicateurs :

\( p_0 \xrightarrow[\color{blue}{\nearrow \,15\,\%}]{} p_1 \xrightarrow[\color{red}{\searrow \,60\,\%}]{} p_2\)

devient :

\( p_0 \xrightarrow{\color{blue}{\times \left( 1 + \dfrac{15}{100}\right)}} p_1 \xrightarrow{\color{red}{\times \left( 1 - \dfrac{60}{100}\right)}} p_2\)

\( p_0 \xrightarrow{\color{blue}{\times 1,15}} p_1 \xrightarrow{\color{red}{\times 0,4}} p_2\)

donc on simplifie :

\( p_0 \xrightarrow{\times 1,15\times 0,4} p_2\) or \( 1,15 \times 0,4 = 0,46 \) donc \( p_0 \xrightarrow{\times 0,46} p_2\)

or \( 0,46 = 1 - 0,54 = 1 - \dfrac{54}{100} \)

cela signifie qu'on a une baisse de 54 %

ligne 3

\( p_0 \xrightarrow[\color{blue}{\searrow \,5\,\%}]{} p_1 \xrightarrow[\color{red}{\nearrow \,5\,\%}]{} p_2\)

devient :

\( p_0 \xrightarrow{\color{blue}{\times \left( 1 - \dfrac{5}{100}\right)}} p_1 \xrightarrow{\color{red}{\times \left( 1 + \dfrac{5}{100}\right)}} p_2\)

\( p_0 \xrightarrow{\color{blue}{\times 0,95}} p_1 \xrightarrow{\color{red}{\times 1,05}} p_2\) donc \( p_0 \xrightarrow{\times 0,9975} p_2\)

or \( 0,9975 = 1 - 0,0025 = 1 - \dfrac{0,25}{100} \)

cela signifie qu'on a une baisse de 0,25 %

ligne 2

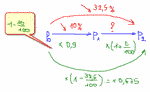
Il faut résoudre \( 0,9 \times \left(1 + \dfrac{t}{100} \right) = 0,675\)

\( \Leftrightarrow 1 + \dfrac{t}{100} = \dfrac{0,675}{0,9}\)

\( \Leftrightarrow \dfrac{t}{100} = \dfrac{0,675}{0,9} - 1\)

\( \Leftrightarrow \dfrac{t}{100} = -0,25\)

\( \Leftrightarrow t = -0,25 \times 100\)

\( \Leftrightarrow t = -25\)

donc une baisse de 25 %