Frédéric Léon -- MATHS -- E. Brontë

▲

Préparation contrôle c07

Lire l'équation réduite d'une droite

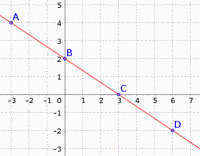
A l'aide d'une lecture graphique, déterminer l'équation réduite de la droite \((AB)\) (Les points indiqués sont à coordonnées entière).

droite dans un repère

Aide
Aide : l'équation réduite d'une droite est de la forme : \(y = mx + p\) donc il faut lire sur le graphique :
  • l'ordonnée à l'origine
  • le coefficient directeur : \( m = \dfrac{\text{déplacement en }y}{\text{déplacement en }x}\)
Solution

Une équation réduite de droite est de la forme \( y = mx + p \)

  • L'ordonnée du point \( B \) est l'ordonnée à l'origine, donc \( p = 2 \)
  • Pour aller de \( B \) à \( C \), on se déplace de 3 unités en abscisses et de 2 unités vers le bas en ordonnées, donc \( \dfrac{\Delta_y}{\Delta_x} = \dfrac{-2}{3} = m \)

L'équation de la droite est donc \( y = -\dfrac{2}{3} x + 2 \)

Déterminer l'équation réduite d'une droite à l'aide d'un calcul

Soient les points \(A ( -2\,; 10) \) et \(B ( 2020\,; -5) \).

Déterminer l'équation de la droite \( (AB) \).

Aide

l'équation réduite d'une droite est de la forme : \(y = mx + p\)

  • première méthode
    • calculer \( m \) à l'aide de la formule \( m = \dfrac{y_B - y_A}{x_B - x_A}\)
    • calculer \( p \) en résolvant une équation traduiant le fait que les coordonnées de \( A \) doivent vérfier l'équation de la droite \( (AB) \)
  • deuxième méthode :

    utiliser la formule : \(y = \dfrac{y_B - y_A}{x_B - x_A}(x -x_A) + y_A\)

Solution
  • méthode 1

    \( m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{-5 - 10}{2020 - (-2)} = \dfrac{-15 }{2022} = \dfrac{-5 }{674} \)

    les coordonnées de \( A \) doivent vérifier : \( y_A = \dfrac{-5 }{674} x_ A + p \).

      \( \phantom{\Leftrightarrow\,} 10 = \dfrac{-5 }{674} \times (-2) + p \).
    • \( \Leftrightarrow 10 = \dfrac{5 }{337} + p \).
    • \( \Leftrightarrow 10 \color{red}{-\dfrac{5 }{337}} = \dfrac{5 }{337} \color{red}{-\dfrac{5 }{337}} + p \).
    • \( \Leftrightarrow \dfrac{3365 }{337} = p \).

    donc \( y = \dfrac{-5 }{674} x + \dfrac{3365 }{337} \)

  • méthode 2
      \(y = \dfrac{y_B - y_A}{x_B - x_A}(x -x_A) + y_A\)
    • \(y = \dfrac{-5 - 10}{2020 - (-2)}(x - (-2)) + 10\)
    • \(y = \dfrac{-15}{2022}(x + 2) + 10\)
    • \(y = \dfrac{-5}{674}x + \dfrac{-5}{674} \times 2 + 10\)

    donc \( y = \dfrac{-5 }{674} x + \dfrac{3365 }{337} \)

Désolé, mais parfois les calculs font apparaître des fractions qui ne sont pas toujours simplifiables... En cas d'angoisse, ne pas hésiter à utiliser la calculatrice : elle sait travailler avec (certaines) fractions !

Trouver le signe d'une expression produit

Déterminer, en justifiant le raisonnement et les calculs, l'ensemble des réels tels que : \( (2x + 5)(14 - 3x) \geqslant 0 \)
Aide 1

Construire un tableau de signe :

\( \begin{array}{|l|lcr|} \hline \\ x & & \phantom{un peu de place} & \\\hline \text{signe de }(2x + 5) & & & \\\hline \text{signe de }(14 - 3x) & & & \\\hline \text{signe du produit} & & & \\\hline \end{array} \)

Aide 2

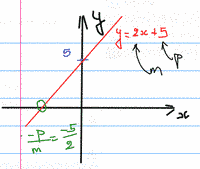
pour déterminer le signe de \( 2x + 5 \), on peut travailler à l'aide d'une fonction : \( f(x) = 2x + 5 \) et chercher le signe de cette fonction.

\( f \) est une fonction affine, donc de la forme \( y = mx + p \) : on peut déterminer les valeurs de \( m \) et \( p \) et se rappeler que la représentation graphique d'une fonction affine est une droite.

Représenter rapidement cette droite afin de déterminer le signe de \( f \) et justifier (par un calcul, ou une formule) que la valeur de \( x \) qui annule la fonction est \( \dfrac{-5}{2} \)

Solution

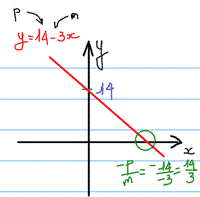
\( \begin{array}{|l|lcccr|} \hline \\ x &-\infty & -\frac{5}{2}& & \frac{14}{3}& +\infty \\\hline \text{signe de }(2x + 5) & - & 0 & + & | & + \\\hline \text{signe de }(14 - 3x) & + & | & + & 0 & - \\\hline \text{signe du produit} & -& 0 & + &0 & -\\\hline \end{array} \) graphique fct 2x+5 graphique fct 14-3x

donc \( (2x+5)(14-3x) \ge 0 \) si \( x \in \left[ -\frac{5}{2}\,; \frac{14}{3}\right] \)

reamarque : donc \( (2x+5)(14-3x) \le 0 \) si \( x \in \left]-\infty \,; -\frac{5}{2}\right] \cup \left[\frac{14}{3}\,; +\infty\right] \)

Utiliser une formule tableur

dans une feuille tableur,

  • la cellule A3 contient le nombre 3 ;
  • la cellule B3 contient la formule : =SI(A3<2 ; A3^2 ; 3*A3 + 5)

Quelle va être la valeur affichée dans la cellule B3 ?

Aide

la fonction SI du tableur fonctionne de la façon suivante : SI( test à affectuer ; action à faire si la réponse au test est "vrai" ; action à faire si la réponse au test est "faux").

ici le test consiste à comparer la valeur de la cellule A3 avec 2

Solution

Comme A3 contient 3, la réponse au test A3<2 est "faux", donc il faut effectuer le calcul 3*A3 + 5

Le résultat affiché dans la cellule B3 sera donc 14.

Résoudre une inéquation à l'aide des fonctions de référence

Résoudre \( 4x^2 + 6 \ge 15 \) en utilisant vos connaissances sur les fonctions de référence.
Aide 1
  1. Il faut se ramener à inéquation équivalente de la forme : \( x^2 \ge \dots \)
  2. Tracer la courbe de la fonction carrée et lire les solutions
Aide 2
  • \( 4x^2 + 6 \ge 15 \Leftrightarrow x^2 \ge \dfrac{9}{4} \)
  • pour \( a \ge 0 \) et \( b > 0 \) : \( \sqrt{\dfrac{a}{b}} = \dfrac{\sqrt{a}}{\sqrt{b}} \)
Solution
    \( 4x^2 + 6 \ge 15 \)
  • \( 4x^2 + 6 \color{red}{-6}\ge 15 \color{red}{-6}\)
  • \( 4x^2 \ge 9\)
  • \( \dfrac{4x^2}{\color{red}{4}} \ge \dfrac{9}{\color{red}{4}}\)
  • \( x^2 \ge \dfrac{9}{4}\)
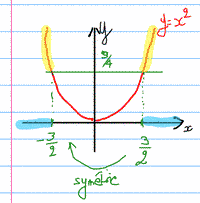
fonction carré et solutions

donc \( 4x^2 + 6 \ge 15 \Leftrightarrow x^2 \ge \dfrac{9}{4} \Leftrightarrow x \in \left]-\infty\,; -\dfrac{3}{2}\right] \cup \left[ \dfrac{3}{2}\,; +\infty \right[ \)