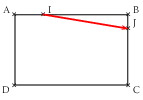
\(ABCD\) est un rectangle.

\({\overrightarrow{AI}} = {\dfrac{1}{4}}{\overrightarrow{AB}}\) ; \({\overrightarrow{BJ}} = {\dfrac{1}{5}}{\overrightarrow{BC}}\).

1.  

2. Exprimer \({\overrightarrow{AC}}\) en fonction de \({\overrightarrow{BA}}\) et \({\overrightarrow{BC}}\) signifie qu’il faut trouver les réels \(\alpha\) et \(\beta\) tels que : \({\overrightarrow{AC}} = \alpha {\overrightarrow{BA}} + \beta {\overrightarrow{BC}}\).

   Une méthode consiste à utiliser la relation de Chasles.

   \({\overrightarrow{AC}} = {\overrightarrow{AB}} + {\overrightarrow{BC}} = - {\overrightarrow{BA}} + {\overrightarrow{BC}}\)

   (ici on vient de trouver \(\alpha = -1\) et \(\beta = 1\)).

3. \({\overrightarrow{IJ}} = {\overrightarrow{IB}} + {\overrightarrow{BJ}}\)

   Or \({\overrightarrow{IB}} = {\dfrac{3}{4}} {\overrightarrow{BA}}\) et \({\overrightarrow{BJ}} = {\dfrac{1}{5}} {\overrightarrow{BC}}\)

   donc \({\overrightarrow{IJ}} = {\dfrac{3}{4}} {\overrightarrow{BA}} + {\dfrac{1}{5}} {\overrightarrow{BC}}\)

4. Le vecteurs sont colinéaires s’il existe un réel \(k\) tel que \({\overrightarrow{IJ}} = k {\overrightarrow{AC}}\).

   Donc on cherche \(k\) tel que \( {\dfrac{3}{4}} {\overrightarrow{BA}} + {\dfrac{1}{5}} {\overrightarrow{BC}} = k \left( - {\overrightarrow{BA}} + {\overrightarrow{BC}}\right)\)

   c’est à dire \( {\color{red}{{\dfrac{3}{4}}}} {\overrightarrow{BA}} + {\color{blue}{{\dfrac{1}{5}}}} {\overrightarrow{BC}} = {\color{red}{- k}} {\overrightarrow{BA}} + {\color{blue}{k}} {\overrightarrow{BC}}\)

   En identifiant, il faut \(\color{red}{k = -{\dfrac{3}{4}}}\) et \(\color{blue}{k = {\dfrac{1}{5}}}\), ce qui est impossible.

   Donc les vecteurs ne sont pas colinéaires (graphiquement les droites \((AC)\) et \((IJ)\) ne semblaient pas parallèles).