Compléments du cours
Première formule
très important \(\log(10^x) = x\)
exemples :
- \(\log(10^2) = 2\) or \(10^2=100\) donc \(\log(100) = 2\)
- \(\log(10^{-3}) = -3\) or \(10^{-3}= 0,001\) donc \(\log(0,001) = -3\)
- par contre pour calculer \(\log(50)\) on utilise la calculatrice.
Remarque
et pour \(\log(100^3)\) ?
la formule ne fonctionne que pour les puissances de \(10\).
- écrire \(100^3\) comme une puissance de \(10\)
- appliquer la formule.
on sait que \(100= 10^2\), donc \(100^3 = (10^2)^3 = 10^{2 \times 3} = 10^6\)
donc \(\log(100^3) = \log(10^6) = 6\)
Deuxième formule
\(a <b\) est équivalent à \(\log(a) < \log(b)\).
Cette formule est utilisée dans les recherche de seuil.
Exemple :
Un capital de \(1\,000\) euros qui est placé à un taux de \(5\,\%\) en intérêts composés.
\(C_n\) est le capital à l'année \(n\).
\(C_0= 1\,000\) ; \(C_1 = 1\,000 \times \left( 1 + \dfrac{5}{100}\right) = 1\,000 \times 1,05 = 1\,050\)
on reconnaît une suite géométrique : \(C_{n+1} = C_n \times 1,05\) (formule par récurrence)
on sait donc que \(C_n = C_0 \times 1,05^n\) (formule explicite)
On cherche le nombre d'années nécessaires pour doubler le capital (comme \(C_0= 1\,000\), on cherche \(n\) tel que \(C_n = 2\,000\).)
à l'aide du tableur
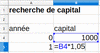on peut copier les formules vers le bas et découvrir que le capital a doublé en 15 ans.
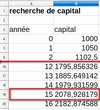
à l'aide des logarithmes
\(C_n= 1\,000 \times 1,05^n\) on cherche \(n\) tel que \(C_n > 2\,000\)
\(1\,000 \times 1,05^n > 2\,000\)
\(\dfrac{1\,000 \times 1,05^n}{\color{red}{1\,000}} > \dfrac{2\,000 }{\color{red}{1\,000}}\)
\(1,05^n > 2\)
donc \(\log(1,05^n) > \log(2)\)
\(\log(1,05^n) > 0,3\)
La suite du cours va donner des formules qui permettent de continuer le calcul...
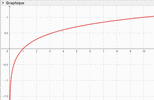
Graphe de la fonction.
La fonction est strictement croissante, mais sa croissance "est très très lente".
On trouve \(y=6\) pour \(x=1\,000\,000\) !
graphe
Signe de la fonction
pour \(x \in ]0\,; 1[\) la fonction est négative ; et positive sinon.
Exercices
p 84 n° 29
\(\begin{array}{lccccc} \hline x & 2 & 3 & 4 & 5 & 6 \\\hline \log(x) & 0,3 & 0,5 & 0,6 & 0,7 & 0,8\\ \hline \end{array}\)
p 86 n° 55
\(\begin{array}{lccccc} \hline x & 0,1 & 1 & 10^2 = 100 & 0,001 & 10^{-5} \\\hline \log(x) & -1 & {\color{blue}{0}} & {\color{red}{2}} & -3 & -5\\ \hline \end{array}\)
pour trouver l'antécédant de \({\color{blue}{0}}\), on sait \(\log(10^x) =x\); donc on a : \(\log(10^x) ={\color{blue}{0}}\) donc il faut avoir \(10^0 = 1\)
pour trouver l'antécédant de \({\color{red}{2}}\), on sait \(\log(10^x) =x\); donc on a : \(\log(10^x) ={\color{red}{2}}\) donc il faut avoir \(10^2 = 100\)