Il existe des inéquations de plusieurs types :
Pour résoudre une inéquation graphiquement, il faut déterminer les abscisses de tous les points se trouvant sur la courbe, dont leur ordonnée est soit supérieure, inférieure et/ou égale à k, selon l'inéquation qu'on a.
On précise que k est un réel quelconque.
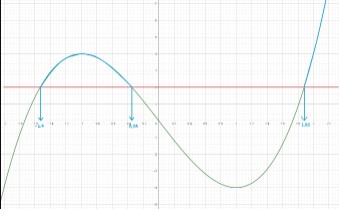
Dans notre exemple ci-dessus, on cherche à résoudre graphiquement l'inéquation suivante : f(x) ≥ 2.
On remarque donc que dans cet exemple, k = 2.
On cherche tous les points de la courbe, ayant une ordonnée supérieure ou égale à 2.
Pour ce faire, il faut d'abord tracer une droite horizontale à l'axe des abscisses, formée de tous les points d'ordonnée k, c'est-à-dire 2 ici.
Une fois la droite réalisée, il faut observer où sont les points de la courbe, ayant une ordonnée supérieure ou égale à 2, donc ceux au dessus de la droite.
Dans notre cas, les solutions sont les abscisses comprises entre -1,4 et -0,28 inclus. Il y a également les solutions des abscisses comprises entre 1,82 inclus et +\(\infty\) exclus.
Ainsi, f(x) ≥ 2 lorsque \(x \in\) [-1,4 ; -0,28] ∪ [1,82 ; +\(\infty\)[
L'équation est donc résolue.