Fonctions dérivées

Tangente à la courbe

Sécante à la courbe

La figure ci-contre représente la sécante à la courbe de la fonction $f$. Cette sécante passe par les points A et B

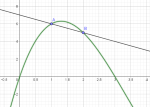
La fonction $f$ est définie sur $\setR$ par $f(x) = \dfrac12 x (x - 3) (x - 7)$ ; les points A et B d'abscisses respectives $x_A = 1$ et $x_B=2$ appartiennent à $\mathscr C_f$ (la courbe de $f$).

Déterminer l'équation de la droite $(AB)$

Aide

L'équation de la droite $(AB)$ est donnée par $y = m (x - x_A) +y_A$ ; avec $m = \dfrac{y_B - y_A}{x_B - x_A}$.
$m$ est le coefficient directeur de la droite $(AB)$.

De la sécante à la tangente

Si le point B est très proche du point A, la sécante se confond avec la tangente.

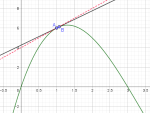
Le coefficient directeur de la tangente est le réel $\ell$ défini par $\ell = \lim\limits_{x_B \to x_A}\dfrac{y_B - y_A}{x_B - x_A} = \lim\limits_{h \to 0}\dfrac{f(x_A + h) - f(x_A)}{h}$

$\ell$ est le nombre dérivé de $f$ en $x_A$ et il se note $f'(x_A)$.

Déterminer l'équation de la tangente à $\mathscr C_f$ au point d'abscisse $x_A = 1$.

Aide 1

Dérivée des fonctions de référence

Fonction	Fonction dérivée
affine : $f(x) = mx + p$	$f'(x) = m$
carrée : $f(x) = x^2$	$f'(x) = 2x$
puissance : $f(x) = x^n$ (avec $n \in \setZ$)	$f'(x) = n \times x^{n-1}$
inverse : $f(x) = \dfrac1x$	$f'(x) = - \dfrac1{x^2}$
racine carrée : $f(x) = \sqrt{x}$	$f'(x) = - \dfrac1{2 \sqrt{x}}$
exponentielle : $f(x) = \e^{x}$	$f'(x) = \e^{x}$
logarithme : $f(x) = \ln{x}$	$f'(x) = \dfrac1x$

Opérations sur les fonctions dérivées

Opération	Fonction dérivée
somme : $f(x) = u(x) + v(x)$	$f'(x) = u'(x) + v'(x) $
produit par un réel $k$ : $f(x) = k \times u(x)$	$f'(x) = k \times u'(x)$
produit de deux fonctions : $f(x) = u(x) \times v(x)$	$f'(x) = u'(x) \times v(x) + u(x) \times v'(x)$
quotient de deux fonctions : $f(x) = \dfrac{u(x)}{v(x)}$	$f'(x) = \dfrac{u'(x) \times v(x) - u(x) \times v'(x)}{(v(x))^2}$
puissance : $f(x) = (u(x))^n$	$f'(x) = n \times u'(x) \times (u(x))^{n-1}$
exponentielle : $f(x) = \e^{u(x)}$	$f'(x) = u'(x) \times \e^{u(x)}$
logarithme : $f(x) = \ln{u(x)}$	$f'(x) = \dfrac{u'(x)}{u(x)}$

Équation de la tangente : $y = f'(x_A) (x - x_A) + f(x_A)$

Aide 2

Pour trouver la fonction dérivée de $f$ :

on peut écrire : $f(x) = \color{blue}{\dfrac12 x} \times \color{red}{(x - 3) (x - 7)}$
on peut développer $f(x)$

Aide 3

Pour vérifier l'expression de la fonction dérivée, on peut utiliser un logiciel de clacul formel (le module Calcul formel de GeoGebra par exemple.

Rappel : il faut écrire f(x) := 1/2 * x * (x - 3) * (x- 7) (affecter par := et écrire tous les signes d'oprations)

puis f'(x)

Applications

Vitesse moyenne / vitesse instantanée

feuille d'exercice

Du signe coefficient directeur de la tangente aux variations de la fonction

Le signe du coefficient directeur de la tangente, c'est à dire le signe du nombre dérivé permet de connaître les variations de la fonction étudiée.

signe de la dérivée
variations de la fonction étudiée

si $f'(x) \geqslant 0$ alors $f$ est croissante.
si $f'(x) \leqslant 0$ alors $f$ est décroissante.

Dérivée et calcul formel
Cet exercice est la suite de l'exercice traité lors du chapitre sur les statistiques à 2 variables
Soit $f$ la fonction définie sur l'intervalle $\intfo0{+\infty}$ par :

\[f(t) = \dfrac{450}{1 + 7\text{e}^{-0,05t}}\]

On admet que cette fonction permet de modéliser l'évolution du nombre de personnes équipées de l'implant médical dans un pays.

Plus précisément, $f(t)$ représente le nombre de personnes, exprimé en milliers, équipées de l'implant médical dans ce pays en fonction du temps $t$ mesuré en années depuis 2013.

Par exemple, $f(1)$ représente le nombre de personnes (en milliers) de ce pays équipées de l'implant médical en 2014.
1. Déterminer, selon ce modèle, combien de personnes, au millier près, seront équipées de l'implant médical en 2026.
2. Déterminer la limite de la fonction $f$ en $+ \infty$. Interpréter le résultat dans le contexte de l'exercice.
  Aide
  Pour nous, les limites se retrouvent par du «bon sens» : pour une limite en $+\infty$, on imagine qu'on calcule avec une très grande valeur de $t$, par exemple $10^{100}$.
3. À l'aide d'un logiciel de calcul formel, on a obtenu l'expression suivante:
  
  \[f'(t) = 1755 \dfrac{\e^{\frac{-1}{20} t}}{156 \e^{\frac{-1}{20} } + 6084 \left(\e^{\frac{-1}{20} t} \right)^2 + 1} \]
  
  En déduire le sens de variation de la fonction $f$ sur l'intervalle $\intfo0{+\infty}$ et l'interpréter dans le contexte de l'exercice.
  Aide
  Le sens de variations de la fonction $f$ est donné par le signe de la fonction dérivée : $f'$.
  
  quelque soit $x \in \setR : \e^x > 0$
4. Soit $g(t) = \e^{-0,05 t}$. Déterminer l'expression de $g'(t)$.
  
  Aide
  $g(t)$ est de la forme $\e^{u(t)}$ qui est une formule connue.
5. En déduire, sans l'aide d'un logiciel, l'expression de $f'(t)$ en remarquant que $f(t)$ est de la forme $\dfrac{u(x)}{v(x)}$ (ou de la forme $k \times \dfrac{1}{v(x)}$ avec $k$ réel).
  
  Est-ce la même expression que celle obtenue par le logiciel ?
  
  Aide
  
  $f(t)$ est de la forme $\dfrac{u(t)}{v(t)}$ avec $u(t) = 450$ et $v(t) = 1 + 7 \e^{-0,05t}$.
  
  $u$ est une fonction constante, donc sa dérivée est nulle.
6. Déterminer à partir de quelle année le nombre de personnes de ce pays équipées de cet implant médical dépassera $\np{120000}$, c'est-à-dire $120$ milliers. On expliquera la méthode employée.
Afin de vérifier la bonne isolation thermique d'un spa, on porte la température de l'eau, du spa à 38°C puis on coupe l'alimentation électrique qui sert à chauffer l'eau.

On s'intéresse à l'évolution de cette température en fonction du temps écoulé à partir de cette coupure.

La température de l'eau du spa est modélisée par une fonction $f$ qui, à tout temps $t$ (en heures) écoulé depuis la coupure de l'alimentation électrique, associe la température $f(t)$, en degré Celsius (°C), de l'eau du spa au temps $t$.

On admet que, pour tout réel $t$ de l'intervalle $\intfo0{+\infty}$, \[f(t) = 13\e^{-0,05t} +25.\]

Lors de cette vérification, la température ambiante extérieure au spa reste constante et égale à $25$°C.
1. 1. Déterminer la température initiale de l'eau du spa, puis la température au bout d'une heure et demie.
    Aide
    La température initiale, c'est la température pour $t=0$/
    
    Une heure et demie correspond à $t = \np{1,5}$.
  2. Calculer la valeur arrondie à $10^{-1}$ de $f(24)$, puis interpréter cette valeur dans le contexte de l'exercice.
2. 1. Pour tout réel $t$ de l'intervalle $\intfo0{+\infty}$, déterminer une expression de $f'(t)$.
    Aide
    
    $f$ est de la forme $k \times \e^{u(t)} + \text{ une constante}$
    
    Solution
    
    $f$ est de la forme $k \times \e^{u(t)} + \text{ une constante}$ avec $k = 13$ et $u(t) = -0,05 t$
    
    On a $u'(t) = -0,05$ et on sait que la dérivée de $x \mapsto \e^u$ est $x \mapsto u' \times \e^u$ ; la dérivée d'une constante est nulle.
    
    donc $f'(x) = 13 \times (-0,05) \times \e^{-0,05 t} = -6,5 \e^{-0,05 t}$
  2. En déduire le sens de variation de la fonction $f$ sur l'intervalle $\intfo0{+\infty}$.
    Aide
    
    le sens de variation est donné par le signe de la fonction dérivée.
3. 1. Déterminer la limite de la fonction $f$ en $+ \infty$.
    
    Interpréter la valeur de cette limite dans le contexte de l'exercice.
    
    Aide
    
    les limites se déterminent avec du bon sens !
    
    quand $t$ tend vers $+\infty$ ; $-0,05 t$ tends vers ...
    
    et donc $\e^{-0,05t}$ tend vers ...
  2. Une alarme sonore est émise quand la température de l'eau du spa devient strictement inférieure à une température programmée par l'utilisateur.
    
    L'utilisateur programme la température de l'eau du spa à 36°C.
    
    Déterminer, par le calcul, combien de temps après la coupure de l'alimentation électrique cette alarme sonore retentira (arrondir le résultat à la minute).
    
    Aide
    
    Il faut résoudre $f(t) \leqslant 36$
On considère la fonction $f$ définie sur $\intfo6{+\infty}$ par $f(x)=300(x - 6)\e^{-\frac{1}{4}x}$.
1. Expliquer pourquoi il vous est impossible de déterminer la limite de $f$ en $+\infty$ ; par la suite, on admet que cette limite est $0$.
2. Montrer que $f'(x)=75(10 - x)\e^{-\frac{1}{4}x}$.
3. Étudier les variations de la fonction $f$ sur l'intervalle $\intfo6{+\infty}$ et donner son tableau de variations.
4. Vérifier les résultats obtenus en traçant la courbe représentative de $f$ à l'aide d'un logiciel ou d'une calculatrice.
Un réservoir contient $60\,\text{m}^3$ d'eau destinée à abreuver du bétail. Dans ce qui suit, $t$ est le temps exprimé en heures.

À l'instant $t = 0$, se déverse dans le réservoir une eau polluée par une substance M. Un système de trop plein permet de conserver à tout instant à partir de l'instant $t = 0$ un volume de $60\,\text{m}^3$ dans le réservoir.

On admet, qu'à l'instant $t$ (exprimé en heures), le volume exprimé en litres, de substance polluante M présente dans le réservoir est donnée par la fonction $v$ définie sur $\intfo0{+\infty}$ par :

\[v(t) = \np{2400}\left(1 - \e^{- 0,01t}\right)\]
1. Déterminer $\lim\limits_{t \to +\infty} v(t)$. Interpréter le résultat dans le contexte de l'exercice.
  
  Aide
  
  les limites se déterminent avec du bon sens !
  
  quand $t$ tend vers $+\infty$ ; $-0,01 t$ tends vers ...
  
  et donc $\e^{-0,01 t}$ tend vers ...
  
  Solution
  
  $\lim\limits_{t \to +\infty} -0,01 t= -\infty$
  
  donc $\color{red}{\lim\limits_{t \to +\infty} \e^{-0,01 t}= 0}$
  
  donc $\lim\limits_{t \to +\infty} f(t)$ est de la forme $\np{2400} \times ( 1 - \color{red}{0}) = \np{2400}$
  
  Au bout de nombreuses heures, $2400$ litres d'eau du réservoir seront polluées.
2. On désigne par $v'$ la fonction dérivée de la fonction $v$.
  1. Donner une expression de $v'(t)$ pour tout $t$ de $\intfo0{+\infty}$.
  2. Construire le tableau de variation de la fonction $v$ sur $\intfo0{+\infty}$.
    Aide
    
    il faut trouver le signe de la fonction dérivée.
3. Résoudre sur $\intfo0{+\infty}$ l'équation $v(t)=1200$.
  Solution
  $\begin{array}{lrl} & v(t) &= 1200 \\ \ssi & \np{2400}\left( 1 - \e^{-0,01 t}\right) &= 1200 \\ \ssi & 1 - \e^{-0,01 t} &= \dfrac12 \\ \ssi & \dfrac12 &= \e^{-0,01 t}\\ \ssi & -\ln(2) &= -0,01 t\\ \ssi & t &= \dfrac{\ln(2)}{0,01} \\ \ssi & t &\approx 69,3 \\ \end{array}$
4. 1. La santé du bétail est menacée lorsque le volume de substance $M$ dans le réservoir atteint $2\,\%$ du volume total du réservoir. Déterminer la valeur de $t$ à partir de laquelle la santé du bétail est menacée par la présence dans le réservoir de substance $M$.
    Aide
    
    $2\,\%$ de $60\,\text{m}^3$ c'est $1,2\,\text{m}^3$
    
    $1\,\text{dm}^3 = 1\,\ell$
  2. Le volume de substance $M$ dans le réservoir peut-il dépasser $4\,\%$ du volume du réservoir ? Justifier la réponse.
Dans une usine, on se propose de tester un nouveau modèle de hotte aspirante pour les laboratoires. Avant de lancer la fabrication en série, on a réalisé l'expérience suivante avec un prototype : dans un local clos de volume $500\,\text{m}^3$, équipé du prototype de hotte aspirante, on diffuse du dioxyde de carbone ($CO_{2}$) à débit constant.

Dans ce qui suit, $t$ est le temps exprimé en minutes. À l'instant $t = 0$, la hotte est mise en marche. Les mesures réalisées permettent d'admettre qu'au bout de $t$ minutes de fonctionnement de la hotte, avec $0 \leqslant t \leqslant 15$, le volume de dioxyde de carbone, exprimé en $\text{m}^3$, contenu dans le local est $f(t)$ avec

\[ f(t) = (4t + 1)\e^{-0,5t}\]
1. Déterminer le volume de dioxyde de carbone, en $\text{m}^3$, présent dans le local au moment de la mise en marche de la hotte aspirante.
  Aide
  
  il faut calculer $f(t)$ pour $t=0$.
2. On désigne par $f'$ la fonction dérivée de la fonction $f$. Vérifier en détaillant les calculs que pour tout nombre réel $t$ de $\intff0{15}, f'(t) = (3,5 - 2t)\e^{-0,5t}$.
  Aide
  
  $f$ est de la forme $u \times v$ avec $u(t) = 3,5 - 2t$ et $v(t) = \e^{-0,5t}$
3. Établir alors le tableau de variation de $f$.
4. Obtenir une représentation graphique de la fonction $f$ à l'aide d'un logiciel ou d'une calculatrice : vérifier que le graphique obtenu est cohérent avec le tableau de variations (appeler pour vérification)
5. L'atmosphère «ordinaire» contient $0,035\,\%$ de dioxyde de carbone.
  1. Déterminer le volume en $\text{m}^3$ de $CO_2$ dans un volume de $500\,\text{m}^3$
  2. Déterminer à l'aide d'une lecture graphique le temps de fonctionnement nécessaire pour le volume de $CO_2$ soit inférieure ou égal à celui de l'atmosphère «oridnaire»