Exercices : Fonctions de référence

• Fonctions affines
• Polynômes du second degré
• Fonctions logarithme et exponentielle
• Problèmes

Fonctions affines

Identifer une fonction affine

Pour chacune des fonctions suivantes, si elle est affine, déterminer la valeur du coefficient directeur, de l'antécédent de $0$ et le sens de variation.

1. • $f(x) = 2 x - 4$
   • $g(x) = 5 - 3x$
   • $h(x) = \dfrac23 x + 5$
   • $i(x) = \dfrac{6 x + 4}3$
   • $j(x) = -\dfrac25 x$
   • $k(x) = -3$
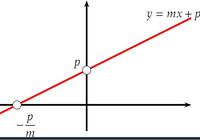
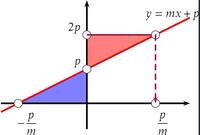
   Aide

   Une fonction affine est définie sur $\setR$ et peut s'écrire sous la forme $f(x) = \color{red}{m} x + \color{blue}{p}$ ($\color{red}{m}$ et $\color{blue}{p}$ étant des réels quelconques).

   • $\color{red}{m}$ est le coefficient directeur, son signe donne le sens de variation de la fonction.
   • $\color{blue}{p}$ est l'ordonnée à l'origine, c'est l'image de $0$, c'est à dire $f(0)=p$.
   • si $m \neq 0$, alors la fonction s'annule en $x_0 = -\dfrac{p}{m}$ ; $x_0$ est l'antécédent de $0$ ; c'est à dire $f\left(-\dfrac{p}{m}\right) = 0$.

   Si besoin, changer l'expression de la fonction afin de l'écrire sous la forme $f(x) = m x + p$

   

   Solution

   • $f(x) = 2 x - 4 = 2x + (-4)$ : donc $m = 2$, on en déduit que la fonction est croissante ; $p=-4$, donc l'antécédent de $0$ est $x_0 = \dfrac{- (-4)}2 = 2$.
   • $g(x) = 5 - 3x = -3x + 5$ : donc $m = -3$, on en déduit que la fonction est décroissante ; $p=5$, donc l'antécédent de $0$ est $x_0 = \dfrac{- 5}{-3} = \dfrac53$.
   • $h(x) = \dfrac23 x + 5$ : donc $m = \dfrac23$, on en déduit que la fonction est croissante ; $p=5$, donc l'antécédent de $0$ est $x_0 = \dfrac{- 5}{\frac23} = -\dfrac{15}2$.
   • $i(x) = \dfrac{6 x + 4}3 = \dfrac63 x + \dfrac43 = 2x + \dfrac43$ : donc $m = 2$, on en déduit que la fonction est croissante ; $p=-\dfrac43$, donc l'antécédent de $0$ est $x_0 = \dfrac{-\frac43}{2} = -\dfrac23$.
   • $j(x) = -\dfrac25 x = -\dfrac25 x + 0$ : donc $m = -\dfrac25$, on en déduit que la fonction est décroissante ; $p=0$, donc l'antécédent de $0$ est $x_0 = 0$. ($j$ est une fonction linéaire)
   • $k(x) = -3 = 0 x + (-3)$: donc $m = 0$, on en déduit que la fonction est constante ; $p=-3$, donc $0$ n'a pas d'antécédent.
2. • $f(x) = 3 x + 7$
   • $g(x) = 2 x^2 + 6$
   • $h(x) = \dfrac{4x + x^2}{x}$
   • $i(x) = x^2 + (3 + x)(5 - x)$
   • $j(x) = \dfrac{2 + 7x}3$
   • $k(x) = -0,3 x + 2,7$
   Solution

   • $f(x) = 3 x + 7$ : donc $m = 3$, on en déduit que la fonction est croissante ; $p=7$, donc l'antécédent de $0$ est $x_0 = \dfrac{- 7}3$.
   • $g(x) = 2 x^2 + 6$ : n'est pas de la forme $g(x) = mx + p$, ce n'est pas une fonction affine.
   • $h(x) = \dfrac{4x + x^2}{x}$ : n'est pas définie pour $x = 0$, ce n'est donc pas une fonction affine (sa représentation graphique est la réunion de deux demi-droite, il y a un "trou" pour $x = 0$).
   • $i(x) = x^2 + (3 + x)(5 - x) = x^2 + 15 + 2x - x^2 = 2x + 15$ : donc $m = 2$, on en déduit que la fonction est croissante ; $p=15$, donc l'antécédent de $0$ est $x_0 = \dfrac{-15}{2}$.
   • $j(x) = \dfrac{2 + 7x}3 = \dfrac73 x + \dfrac23$ : donc $m = \dfrac73$, on en déduit que la fonction est croissante ; $p=\dfrac23$, donc l'antécédent de $0$ est $x_0 = \dfrac{-\frac23}{\frac73} = -\dfrac27$.
   • $k(x) = -0,3x + 2,7$: donc $m = -0,3$, on en déduit que la fonction est décroissante ; $p=2,7$, donc l'antécédent de $0$ est $x_0 = \dfrac{-2,7}{-0,3} = 9$.
3. • $f(x) = 7 + x^2$
   • $g(x) = \dfrac{2 x + 6}5$
   • $h(x) = \dfrac{x^2 + x}{x + 1}$
   • $i(x) = (3x + 1)(x - 4) - 3x^2$
   • $j(x) = 4x + 30$
   • $k(x) = 3 \cdot 10^{-3} x - 33 \cdot 10^{-2}$

   On considère les fonctions de la dernière série. Clique ici pour écrire le nombre de fonctions affines croissantes qui ont un antécédent de $0$ inférieur ou égal à $5$.

Application à la biochimie

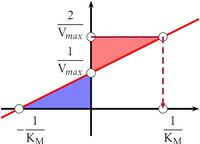
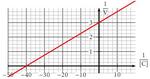
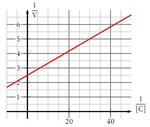
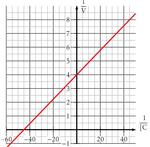
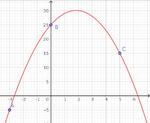
Chaque droite suivante est une représentation de Lineweaver-Burke, dite en double inverse, de l’équation de Michaelis, grâce à la quelle il est possible de déterminer $V_{max}$ et $K_M$.

1. 
   Aide

   

   Remarque : les triangles rouge et bleu étant symétriques, on en déduit que l'antécédent de $2p$ et $\dfrac{p}{m}$. (On peut retrouver ce résultat par le calcul.)

   Le même schéma, mais avec des notations adaptées aux exercices de bio-chimie ($p=\ffrac1{V_{max}}$ et $-\ffrac{p}{m} = -\ffrac1{K_M}$).

   

   Solution

   On place $\ffrac2{V_{max}}=2$, puis on lit $\ffrac1{K_M} = 80$ ; donc $V_{max} = 1$ et $K_M = \ffrac1{80} = \np{0,0125}$.

2. 
   Solution

   On lit $\ffrac1{V_{max}}=3$, donc $V_{max} \approx \np{0,33}$ puis on lit $-\ffrac1{K_M} = -40$, donc $K_M = \ffrac1{40} = \np{0,025}$.

3. 
   Solution

   On lit $\ffrac1{V_{max}}=\np{2,5}$, donc $V_{max} = \np{0,2}$ puis on lit $\ffrac1{K_M} = 30$, donc $K_M \approx \np{0,033}$.

4. 

   On considère la dernière droite de cette série. Clique ici pour écrire les trois derniers chiffres de la valeur approchée au millième de $K_M$.

Déterminer une équation

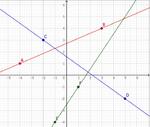
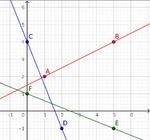
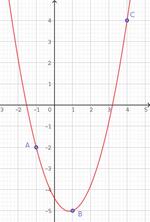
Pour chaque fonction affine représentée par la droite passant par les points marqués (ils sont à coordonnées entières), déterminer l'intervalle sur lequel elle est positive.

1. 

   Aide

   La droite $(AB)$ passant par les points $\color{red}{A(x_A\,;y_A)}$ et $\color{blue}{B(x_B\,; y_B)}$ est la représentation de la fonction affine $f(x) = mx + p$

   On peut trouver son expression à partir de $f(x) = m (x - \color{red}{x_A}) + \color{red}{y_A}$ avec $m = \dfrac{\color{blue}{y_B} - \color{red}{y_A}} {\color{blue}{x_B} - \color{red}{x_A}}$

   Remarque : on trouve la même équation réduite à partir de $f(x) = m (x - \color{blue}{x_B}) + \color{blue}{y_B}$.

   Solution

   • droite $(AB)$ :

     $f(x) = \dfrac{\color{blue}{4} - \color{red}{1}} {\color{blue}{3} - \color{red}{(-4)}} (x - \color{red}{(-4)}) + \color{red}{1} = \dfrac37(x + 4) + 1 = \dfrac37x + \dfrac{19}{7}$ :

     donc la fonction s'annule en $x_0 = \dfrac{-\frac{19}7}{\frac37} = -\dfrac{19}3$ ; comme $m = \dfrac37 > 0$, elle est positive sur $\intfo{-\dfrac{19}3}{+\infty}$.

   • droite $(CD)$ :

     $f(x) = \dfrac{\color{blue}{-2} - \color{red}{3}} {\color{blue}{-5} - \color{red}{(-2)}} (x - \color{red}{(-2)}) + \color{red}{3} = -\dfrac57(x + 2) + 3 = -\dfrac57x + \dfrac{11}{7}$ :

     donc la fonction s'annule en $x_0 = \dfrac{-\frac{11}7}{-\frac57} = \dfrac{11}5$ ; comme $m = -\dfrac57 < 0$, elle est positive sur $\intof{-\infty}{\dfrac{11}5}$.

   • droite $(EF)$ :

     $f(x) = \dfrac{\color{blue}{-1} - \color{red}{(-4)}} {\color{blue}{1} - \color{red}{(-1)}} (x - \color{red}{(-1)}) + \color{red}{(-4)} = \dfrac32(x + 1) - 4 = \dfrac32x - \dfrac52$ :

     donc la fonction s'annule en $x_0 = \dfrac{-\left( -\frac52 \right)}{\frac32} = \dfrac53$ ; comme $m = \dfrac32 > 0$, elle est positive sur $\intfo{\dfrac53}{+\infty}$.

2. 

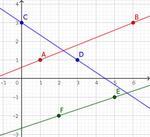
   Solution

   • droite $(AB)$ :

     $f(x) = \dfrac{\color{blue}{4} - \color{red}{2}} {\color{blue}{5} - \color{red}{1}} (x - \color{red}{1}) + \color{red}{2} = \dfrac12(x - 1) + 2 = \dfrac12x + \dfrac32$ :

     donc la fonction s'annule en $x_0 = \dfrac{-\frac32}{\frac12} = -3$ ; comme $m = \dfrac12 > 0$, elle est positive sur $\intfo{-3}{+\infty}$.

   • droite $(CD)$ :

     $f(x) = \dfrac{\color{blue}{-1} - \color{red}{4}} {\color{blue}{2} - \color{red}{0}} (x - \color{red}{0}) + \color{red}{4} = -\dfrac52 x + 4$ :

     donc la fonction s'annule en $x_0 = \dfrac{-4}{-\frac52} = \dfrac85$ ; comme $m = -\dfrac52 < 0$, elle est positive sur $\intof{-\infty}{\dfrac85}$.

   • droite $(EF)$ :

     $f(x) = \dfrac{\color{blue}{-1} - \color{red}{1}} {\color{blue}{5} - \color{red}{0}} (x - \color{red}{0}) + \color{red}{1} = -\dfrac25 x + 1$ :

     donc la fonction s'annule en $x_0 = \dfrac{-1}{-\frac25} = \dfrac52$ ; comme $m = -\dfrac25 < 0$, elle est positive sur $\intof{-\infty}{\dfrac52}$.

3. 

   On considère les fonctions de la dernière série. Clique ici pour écrire le produit des bornes réelles de chaque intervalle.

Polynômes du second degré

Inéquations du second degré

Pour chacune des fonctions suivantes :

• Déterminer les coordonnées du sommet de la parabole
• Résoudre $f(x) \geq 0$

1. • $f(x) = x^2 - 4x + 5$
   • $g(x) = 3x - 2 x^2 + 1$
   • $h(x) = 4x^2 + 5x - 3$
   • $i(x) = 9x^2 - 4$
   Aide

   Un polynôme du second degré est une fonction de la forme $f(x) = ax^2 + bx + c$ avec $a$, $b$ et $c$ réels et $a \neq 0$.

   Il est prudent de commencer par trouver les valeurs des coefficients !

   Sa représentation graphique est une parabole ; l'orientation de la parabole est donnée par le signe de $a$ (le coefficient de $x^2$).

   Les racines $x_1$ et $x_2$ du polynôme (valeurs qui annulent ; intersection avec l'axe des abscisses) sont données par : $x_1 = \dfrac{-b - \sqrt{\Delta}}{2a}$ et $x_2 = \dfrac{-b + \sqrt{\Delta}}{2a}$ avec $\Delta = b^2 - 4ac$.

   Remarques :

   • Si $\Delta < 0$, alors $x_1$ et $x_2$ n'existent pas !
   • Si $\Delta = 0$, alors $x_1 = x_2$
   • Si $\Delta > 0$, alors on peut factoriser $f$ en $f(x) = a (x - x_1)(x - x_2)$

   La parabole est une courbe qui admet l'axe d'équation $x = -\dfrac{b}{2a}$ comme axe de symétrie (c'est la moyenne des deux racines : $\dfrac{x_1 + x_2}2$).

   En posant $\alpha = -\dfrac{b}{2a}$, le sommet de la parabole a pour coordonnées $\left( \alpha \,; f\left(\alpha\right)\right)$

   Remarque : un schéma rapide permet de vérifier les calculs !

   Solution

   • $f(x) = x^2 - 4x + 5$ : donc $\color{red}{a = 1}$, $\color{blue}{b=-4}$ et $\color{green}{c=5}$.

     Comme $\color{red}{a} > 0$, on en déduit que la parabole est orientée « vers le haut  »

     $\alpha = - \dfrac{b}{2a} = - \dfrac{\color{blue}{-4}}{2 \times \color{red}{1}} = 2$ ; donc le sommet de la parabole a pour coordonnées $(2 \,; 1)$

     $\Delta = (\color{blue}{-4})^2 - 4 \times \color{red}{1} \times \color{green}{5} = -4$ ; donc la fonction n'admet pas de racine : la parabole ne coupe pas l'axe des abscisses ; la fonction est strictement positive.

     

   • $g(x) = 3x - 2x^2 + 1 = -2x^2 + 3x + 1$ : donc $\color{red}{a = -2}$, $\color{blue}{b=3}$ et $\color{green}{c=1}$.

     Comme $\color{red}{a} < 0$, on en déduit que la parabole est orientée « vers le bas  »

     $\alpha = - \dfrac{b}{2a} = - \dfrac{\color{blue}{3}}{2 \times \color{red}{(-2)}} = \dfrac34$ ; donc le sommet de la parabole a pour coordonnées $\left(\dfrac34 \,; \dfrac{17}8 \right)$

     $\Delta = \color{blue}{3}^2 - 4 \times \color{red}{(-2)} \times \color{green}{1} = 17$ ; donc la fonction admet deux racines : $x_1 = \dfrac{-\color{blue}{3} - \sqrt{17}}{2 \times \color{red}{(-2)}} = \dfrac{3 + \sqrt{17}}{4} \approx 1,78$ et $x_2 = \dfrac{3 - \sqrt{17}}{4} \approx -0,28$

     $f(x) \geq 0 \Leftrightarrow x \in \intff{x_2}{x_1}$

     

   • $h(x) = 4x^2 + 5x - 3$ : donc $\color{red}{a = 4}$, $\color{blue}{b=5}$ et $\color{green}{c=-3}$.

     Comme $\color{red}{a} > 0$, on en déduit que la parabole est orientée « vers le haut  »

     $\alpha = - \dfrac{b}{2a} = - \dfrac{\color{blue}{5}}{2 \times \color{red}{4}} = -\dfrac58$ ; donc le sommet de la parabole a pour coordonnées $\left(-\dfrac58 \,; -\dfrac{73}{16} \right)$

     $\Delta = \color{blue}{5}^2 - 4 \times \color{red}{4} \times \color{green}{(-3)} = 73$ ; donc la fonction admet deux racines : $x_1 = \dfrac{-\color{blue}{5} - \sqrt{73}}{2 \times \color{red}{4}} = \dfrac{-5 - \sqrt{73}}{8} \approx -1,69$ et $x_2 = \dfrac{-5 + \sqrt{73}}{8} \approx 0,44$

     $f(x) \geq 0 \Leftrightarrow x \in \intof{-\infty}{x_1} \cup \intfo{x_2}{+\infty}$

     

   • $i(x) = 9x^2 - 4$ : donc $\color{red}{a = 9}$, $\color{blue}{b=0}$ et $\color{green}{c=-4}$.

     Comme $\color{red}{a} > 0$, on en déduit que la parabole est orientée « vers le haut  »

     On peut reprendre les raisonnements précédents, mais il est plus astucieux de reconnaître l'identité remarquable : $A^2 - B^2 = (A - B)(A + B)$ avec $A = 3x$ et $B = 2$ ; on en déduit que $f(x) = (3x -2)(3x + 2)$

     Les racines sont $x_1 = \dfrac23$ et $x_2 = -\dfrac23$ ; l'abscisse du sommet est $\dfrac{x_1 + x_2}2 = 0$

     Donc le sommet de la parabole a pour coordonnées $\left(0 \,; -4 \right)$

     $f(x) \geq 0 \Leftrightarrow x \in \intof{-\infty}{x_1} \cup \intfo{x_2}{+\infty}$

     

2. • $f(x) = -x^2 + x + 2$
   • $g(x) = x^2 + 6x + 9$
   • $h(x) = 5x - 16x^2$
   • $i(x) = -2x^2 + 4x - 10$
   Solution

   • $f(x) = -x^2 + x + 2$ : donc $\color{red}{a = -1}$, $\color{blue}{b=1}$ et $\color{green}{c=2}$.

     Comme $\color{red}{a} < 0$, on en déduit que la parabole est orientée « vers le bas  »

     On peut reprendre les méthodes précédentes, mais il est plus astucieux de remarquer que les racines sont évidentes : $x_1 = -1$ et $x_2 = 2$

     L'abscisse du sommet de la parabole est $\dfrac{x_1 + x_2}2 = - \dfrac12$ donc le sommet de la parabole a pour coordonnées $\left(-\dfrac12 \,; \dfrac94 \right)$

     $\Delta = (\color{blue}{-4})^2 - 4 \times \color{red}{1} \times \color{green}{5} = -4$ ; donc la fonction n'admet pas de racine : la parabole ne coupe pas l'axe des abscisses ; la fonction est strictement positive.

     $f(x) \geq 0 \Leftrightarrow x \in \intff{x_1}{x_2}$

     

   • $g(x) = x^2 + 6x + 9$ : donc $\color{red}{a = 1}$, $\color{blue}{b=6}$ et $\color{green}{c=9}$.

     Comme $\color{red}{a} > 0$, on en déduit que la parabole est orientée « vers le haut  »

     On peut reprendre les méthodes précédentes, mais il est plus astucieux de remarquer l'identité remarquable $A^2 + 2AB + B^2 = (A + B)^2$ avec $A = x$ et $B=3$.

     donc $f(x) = (x + 3)^2$ : il y a une unique racine $x_0 = -3$, les coordonnées du sommet sont donc $(-3\,; 0)$.

     $f(x) \geq 0 \Leftrightarrow x \in \setR$

     

   • $h(x) = 5x - 16x^2= -16x^2 + 5x$ : donc $\color{red}{a = -16}$, $\color{blue}{b=5}$ et $\color{green}{c=0}$.

     Comme $\color{red}{a} < 0$, on en déduit que la parabole est orientée « vers le bas  »

     On peut reprendre les méthodes précédentes, mais il est plus astucieux de remarquer que $f(x) = x (-16x + 5)$ : on a donc deux racines $x_1 = 0$ et $x_2 = \dfrac5{16}$ (ce sont les valeurs qui annulent $f$).

     $\alpha = \dfrac{x_1 + x_2}2 = \dfrac5{32}$ ; donc le sommet de la parabole a pour coordonnées $\left(\dfrac5{16} \,; \dfrac{25}{64} \right)$

     $f(x) \geq 0 \Leftrightarrow x \in \intff{0}{\dfrac5{16}}$

     

   • $i(x) = -2x^2 + 4x - 10$ : donc $\color{red}{a = -2}$, $\color{blue}{b=4}$ et $\color{green}{c=-10}$.

     Comme $\color{red}{a} < 0$, on en déduit que la parabole est orientée « vers le bas  »

     $\alpha = - \dfrac{b}{2a} = - \dfrac{\color{blue}{4}}{2 \times \color{red}{(-2)}} = 1$ ; donc le sommet de la parabole a pour coordonnées $(1 \,; -8)$

     $\Delta = \color{blue}{4}^2 - 4 \times \color{red}{(-2)} \times \color{green}{(-10)} = -64$ ; donc la fonction n'admet pas de racine : la parabole ne coupe pas l'axe des abscisses ; la fonction est strictement négative.

     L'inéquation $f(x) \geq 0$ n'admet pas de solution.

     

3. • $f(x) = -x^2 + 6x -9$
   • $g(x) = -7x^2 + 4x$
   • $h(x) = 9x^2 + 27x - 36$
   • $i(x) = -2x^2 + 8x - 10$

   On considère les fonctions de la dernière série. Clique ici pour écrire la somme des racines entières des fonctions.

Équation d'une parabole

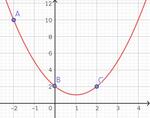
Pour chacune des paraboles suivantes, à l'aide d'une lecture graphique (les points signalés sont à coordonnées entières), déterminer son équation sous la forme $f(x) = ax^2 + bx + c$

1. 

   

   

   Aide

   Un polynôme du second degré est une fonction de la forme $f(x) = ax^2 + bx + c$ avec $a$, $b$ et $c$ réels et $a \neq 0$, donc $f(0) = c$

   Si un point $A(x_A\,; y_A)$ appartient à la courbe représentative de la fonction $f$, alors $f(x_A) = y_A$.

   Si la parabole coupe l'axe des abscisse en $x_1$ et $x_2$, alors on peut factoriser $f$ en $f(x) = a (x - x_1)(x - x_2)$

Solution

• Courbe 1

  La parabole passe par $B(0\,; 2)$, donc $f(0) = 2 = c$. On en déduit que $f(x) = ax^2 + bx + 2$.

  Le point $A(-2\,; 10)$ permet d'écrire $f(-2) = 10 \Leftrightarrow 4a - 2b + 2 = 10 \Leftrightarrow 2a - b = 4$

  Le point $C(2\,; 2)$ permet d'écrire $f(2) = 2 \Leftrightarrow 4a + 2b + 2 = 2 \Leftrightarrow 2a + b = 0$

  Il faut résoudre le système : $\left\lbrace \begin{array}{rcl} 2a - b & = & 4 \\ 2a + b & = & 0 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 2a & = & \color{red}{4 + b}\\ \color{red}{4 + b} + b & = & 0 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 2a & = & 4 + \color{blue}{(-2)} = 2\\ b & = & \color{blue}{-2} \end{array}\right.$

  Donc $a=1$, $b=-2$ et $c=2$, d'où $f(x) = x^2 -2x + 2$ (on peut tracer la fonction pour vérifier !)

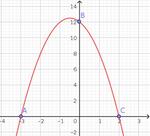
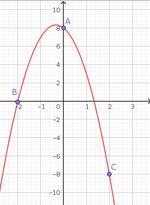
• Courbe 2

  La parabole passe par $B(0\,; 12)$, donc $f(0) = 12 = c$. On en déduit que $f(x) = ax^2 + bx + 12$.

  Les abscisses des points $A$ et $C$ sont les racines du polynôme, donc $f(x) = a (x - x_A)(x - x_C) = a (x - (-3))(x - 2) = a (x + 3)(x -2)$

  On sait que $f(0) = 12 \Leftrightarrow a (0 + 3)(0 -2) = 12 \Leftrightarrow - 6 a = 12 \Leftrightarrow a = -2$

  donc $f(x) = -2 (x + 3) ( x -2) = -2x^2 - 2x + 12$

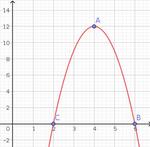
• Courbe 3

  Les abscisses des points $B$ et $C$ sont les racines du polynôme, donc $f(x) = a (x - x_B)(x - x_C) = a (x - 2)(x - 6)$

  Grâce au point $A$, on sait que $f(4) = 12 \Leftrightarrow a (4 - 2)(4 -6) = 12 \Leftrightarrow -4 a = 12 \Leftrightarrow a = -3$

  donc $f(x) = -3 (x - 2) (x - 6) = -3x^2 + 24x - 36$

2. 

   

   

   Solution

   • Courbe 4

     La parabole passe par $A(0\,; 8)$, donc $f(0) = 8 = c$. On en déduit que $f(x) = ax^2 + bx + 8$.

     Le point $B(-2\,; 0)$ permet d'écrire $f(-2) = 0 \Leftrightarrow 4a - 2b + 8 = 0 \Leftrightarrow 2a - b = -4$

     Le point $C(2\,; -8)$ permet d'écrire $f(2) = -8 \Leftrightarrow 4a + 2b + 8 = -8 \Leftrightarrow 2a + b = -8$

     Il faut résoudre le système : $\left\lbrace \begin{array}{rcl} 2a - b & = & -4 \\ 2a + b & = & -8 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 2a & = & \color{red}{-4 + b}\\ \color{red}{-4 + b} + b & = & -8 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 2a & = & -4 + \color{blue}{(-2)} = -6\\ b & = & \color{blue}{-2} \end{array}\right.$

     Donc $a=-3$, $b=-2$ et $c=8$, d'où $f(x) = -3x^2 -2x + 8$ (on peut tracer la fonction pour vérifier !)

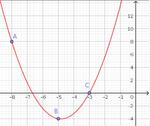
   • Courbe 5

     La parabole passe par $A(-8\,; 8)$, donc $f(-8) = 8 \Leftrightarrow 64 a - 8 b + c = 8$.

     La parabole passe par $B(-5\,; -4)$, donc $f(-5) = -4 \Leftrightarrow 25 a - 5 b + c = -4$.

     La parabole passe par $C(-3\,; 0)$, donc $f(-3) = 0 \Leftrightarrow 9 a - 3 b + c = 0$.

     Il faut résoudre le système : $\left\lbrace \begin{array}{rcl} 64 a - 8 b + c & = & 8 \\ 25 a - 5 b + c & = & -4 \\ 9 a - 3 b + c &=& 0 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 64 a - 8 b + \color{red}{(-9 a + 3 b)} & = & 8 \\ 25 a - 5 b + \color{red}{(-9 a + 3 b)} & = & -4 \\ c &=& \color{red}{-9 a + 3 b} \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 55 a - 5 b & = & 8 \\ 16 a - 2 b & = & -4 \\ c &=& -9 a + 3 b \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 55 a - 5 b & = & 8 \\ 8 a - b & = & -2 \\ c &=& -9 a + 3 b \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 55 a - 5 (\color{blue}{8a + 2}) & = & 8 \\ b & = & \color{blue}{8a + 2} \\ c &=& -9 a + 3 b \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} 15 a - 10 & = & 8 \\ b & = & \color{blue}{8a + 2} \\ c &=& -9 a + 3 b \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} a & = & \dfrac{18}{15} = \dfrac65 \\ b & = & \color{blue}{8a + 2} \\ c &=& -9 a + 3 b \end{array}\right.$

     donc $a = \dfrac65$, $b=\dfrac{58}5$ et $c=24$ ; $f(x) = \dfrac65 x^2 + \dfrac{58}5 x + 24$

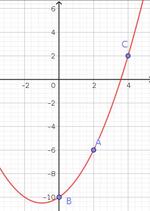
   • Courbe 6

     La parabole passe par $B(0\,; -10)$, donc $f(0) = -10 = c$. On en déduit que $f(x) = ax^2 + bx - 10$.

     Le point $A(2\,; -6)$ permet d'écrire $f(2) = -6 \Leftrightarrow 4a + 2b - 10 = -6 \Leftrightarrow 2a + b = 2$

     Le point $C(4\,; 2)$ permet d'écrire $f(4) = 2 \Leftrightarrow 16a + 4b - 10 = 2 \Leftrightarrow 4a + b = 3$

     Il faut résoudre le système : $\left\lbrace \begin{array}{rcl} 2a + b & = & 2 \\ 4a + b & = & 3 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} b & = &\color{red}{2 - 2a} \\ 4a + \color{red}{2 - 2a} & = & 3 \end{array}\right. \Leftrightarrow \left\lbrace \begin{array}{rcl} b & = & 2 - 2a \\ 2a + 2 & = & 3 \end{array}\right.$

     Donc $a=\dfrac12$, $b=1$ et $c=-10$, d'où $f(x) = \dfrac12x^2 + x -10$

3. 

   

   

   On considère les fonctions de la dernière série. Clique ici pour écrire la somme des somme des neuf coefficients de ces trois polynômes.

Fonctions Logarithme et exponentielle

Calculs et signe

Pour chacune des expressions suivantes :

1. Déterminer son signe sur $\setR$
2. La développer et la simplifier

1. • $A = \e^x \left( \e^x + 5\right)$
   • $B = \e^{-x} \left( \e^x + 2\right)$
   • $C = \e^{2x} \left( \e^x - \e^{-x}\right)$
   Aide

   La fonction exponentielle

   • La fonctions exponentielle est strictement croissante et strictement positive sur $\setR$ ; donc quelque soient les réels $x$ et $y$ :
     • $\e^x > 0$
     • $x < y \Leftrightarrow \e^x < \e^y$
   • Les règles sur les puissances sont étendues aux réels :
     • $\e^0 = 1$ ; $\e^1 = \e$;
     • $\e^x \times \e^y = \e^{x + y}$ ;
     • $\e^{-x} = \dfrac1{\e^x}$ ; $\dfrac{\e^x}{\e^y} = \e^{x-y}$;
     • $\left( \e^x \right)^y = \e^{x \times y}$

   

   Signe d'une expression

   pour trouver le signe d'une expression, on utilise souvent la forme factorisée afin d'appliquer la règle des signes d'un produit.

   Parfois il faut construire un tableau de signes.

   Solution

   • Expression A

     Pour tout $x \in \setR : \e^x > 0$, donc $\e^x + 5 > 0$ ; on en déduit que pour tout $x \in \setR : A > 0$.

     $\begin{align*} & A = \e^x \left( \e^x + 5\right) \\ \Leftrightarrow & A = \e^x \times \e^x + \e^x \times 5 \\ \Leftrightarrow &A = \e^{2x} + 5\e^x \end{align*}$

   • Expression B

     Pour tout $y \in \setR : \e^y > 0$, donc pour $y = -x$ on a $\e^{-x} > 0$ ; et pour tout $x \in \setR$ : $\e^x + 2 > 0$.

     Donc pour tout $x \in\setR : B > 0$.

     $\begin{align*} & B = \e^{-x} \left( \e^x + 2\right) \\ \Leftrightarrow & B = \e^{-x} \times \e^x + \e^{-x} \times 2 \\ \Leftrightarrow & B = \e^{0} + 2 \e^{-x} \\ \Leftrightarrow & B = 1 + 2 \e^{-x} \end{align*}$

   • Expression C

     Pour tout $y \in \setR : \e^y > 0$, donc pour $y = 2x$ on a $\e^{2x} > 0$ ;

     Pour trouver le signe de $\e^x - \e^{-x}$ on cherche $x \in \setR$ tel que :

     $\begin{align*} & \e^x - \e^{-x} > 0 \\ \Leftrightarrow & \e^x > \e^{-x}\\ \Leftrightarrow & x > -x\\ \Leftrightarrow & 2x > 0\\ \Leftrightarrow & x > 0 \end{align*}$

     Donc $C > 0 \Leftrightarrow x \in \intoo0{+\infty}$.

     $\begin{align*} & C = \e^{2x} \left( \e^x - \e^{-x}\right) \\ \Leftrightarrow & C = \e^{2x} \times \e^x - \e^{2x} \times \e^{-x} \\ \Leftrightarrow & C = \e^{3x} - \e^{x} \end{align*}$

2. • $A = \left( \e^x -2 \right)^2$
   • $B = (x + 7)(\e^x - 1)$
   • $C = \left( \e^x - 1 \right)\left( \e^x + 3 \right)$
   Solution

   • Expression A

     $A$ est un carré, donc pour tout $x \in \setR : A \geq 0$.

     $\begin{align*} & A = \left( \e^x -2 \right)^2 \\ \Leftrightarrow & A = \left( \e^x \right)^2 - 2 \times \e^x \times 2 + 2^2\\ \Leftrightarrow &A = \e^{2x} -4 \e^x + 4 \end{align*}$

   • Expression B

     • $x + 7 \geqslant 0 \Leftrightarrow x \geqslant -7$
     • $\e^x - 1 > 0 \Leftrightarrow \e^x > 1 \Leftrightarrow x > 0 $

     $\begin{array}{|l|ccccccc|} \hline x & -\infty & & -7 & & 0 & & +\infty \\\hline \text{signe de }x + 7 & & - & \z & + & \vrule & + & \\\hline \text{signe de }\e^x - 1 & & - & \vrule & - & \z & + & \\\hline \text{signe de }f(x) & & + & \z & - & \z & + & \\\hline \end{array}$

     Donc $B \geq 0 \Leftrightarrow x \in \intof{-\infty}{-7} \cup \intfo0{+\infty}$.

     $B = (x + 7)(\e^x - 1) = x \e^x + 7\e^x - x - 7$

   • Expression C

     Pour tout $x \in \setR : \e^x > 0$, donc $\e^{x} + 3 > 0$ ;

     Pour trouver le signe de $\e^x - 1$ on cherche $x \in \setR$ tel que :

     $\begin{align*} & \e^x - 1 > 0 \\ \Leftrightarrow & \e^x > 1\\ \Leftrightarrow & \e^x > \e^0\\ \Leftrightarrow & x > 0 \end{align*}$

     Donc $C > 0 \Leftrightarrow x \in \setR$.

     $\begin{align*} & C = \left( \e^x - 1\right) \left( \e^x + 3\right) \\ \Leftrightarrow & C = \e^{x} \times \e^x + 3 \e^{x} - \e^{x} - 3\\ \Leftrightarrow & C = \e^{2x} + 2\e^{x} - 3 \end{align*}$

3. • $A = (2x + 5)(\e^x + 3)$
   • $B = \left( \e^x + 1 \right)^2$
   • $C=(-3x + 1)(2\e^x + 1)$

   On considère les expressions de la dernière série. Clique ici pour écrire les bornes de l'intervalle (écrites sous forme de fraction irréductible) sur le quel ces trois expressions sont positives en les séparant par _, par exemple pour $\intff{-\dfrac23}{4,5}$ écrire "-2sur3_9sur2".

Inéquations

1. • $\ln(x) - 3 > 1$
   • $1,25^n > 3$
   • $0,75^n < 0,25$
   • $\e^{x + 2} > 4$
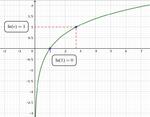
   Aide

   La fonction logarithme népérien

   • La fonction logarithme népérien (notée $\ln$) est strictement croissante sur $\intoo0{+\infty}$ ; elle s'annule en $1$.
     • $\ln(1)= 0$ ; $\ln(0)$ N'EXISTE PAS !!
     • $x < y \Leftrightarrow \ln(x) < \ln(y)$

   • Règles de calculs

     • $\ln(1) = 0$ ; $\ln(\e) = 1$;
     • $\ln(x \times y) = \ln(x) + \ln(y)$ ;
     • $\ln\left( \dfrac1x \right) = -\ln(x)$ ; $\ln\left( \dfrac{x}{y} \right) = \ln(x) - \ln(y)$;
     • $\ln\left( x^y \right) = y \ln(x)$

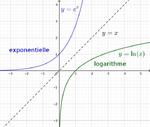
   • la fonction logarithme est la réciproque de la fonction exponentielle donc :

     • pour tout $x \in \setR : \ln \left( \e^x \right) = x$
     • pour tout $x \in \intoo0{+\infty} : \e^{\ln(x)} = x$
     • leurs courbes sont symétriques par rapport à la première bissectrice du repère.

   

   La fonction logarithme décimal

   • La fonction logarithme décimal (notée $\log$ ou parfois $\log_{10}$) est strictement croissante sur $\intoo0{+\infty}$ ; elle s'annule en $1$.
     • $\log(1) = 0$; $\log(10)= 1$ ; $\log(0)$ N'EXISTE PAS !!
     • $x < y \Leftrightarrow \log(x) < \log(y)$
   • Règles de calculs : les mêmes que la fonction logarithme népérien.

   • la fonction logarithme est la réciproque de la fonction $x \mapsto 10^x$ donc :

     • pour tout $x \in \setR : \log \left( 10^x \right) = x$
     • pour tout $x \in \intoo0{+\infty} : 10^{\log(x)} = x$

   

   Solution

   •  

     $\begin{align*} & \ln(x) - 3 > 1 \\ \Leftrightarrow & \ln(x) > 4 \\ \Leftrightarrow & \e^{\ln(x)} > \e^4\\ \Leftrightarrow & x > \e^4 \approx 54,60 \end{align*}$

     Donc $\ln(x) - 3 > 1 \Leftrightarrow x \in \intoo{\e^4}{+\infty}$

   •  

     $\begin{align*} & 1,25^n > 3 \\ \Leftrightarrow & \ln(1,25^n) > \ln(3) \\ \Leftrightarrow & n\ln(1,25) > \ln(3)\\ \Leftrightarrow & n > \dfrac{\ln(3)}{\ln(1,25)} \approx 4,92 \end{align*}$

     Donc $1,25^n > 3 \Leftrightarrow x \in \intoo{\dfrac{\ln(3)}{\ln(1,25)}}{+\infty}$

   •  

     $\begin{align*} & 0,75^n < 0,25 \\ \Leftrightarrow & \ln\left(0,75^n\right) < \ln(0,25) \\ \Leftrightarrow & n \ln(0,75) < \ln(0,25)\\ \Leftrightarrow & n \color{red}{>} \dfrac{\ln(0,25)}{\ln(0,75)} \approx 4,82 \end{align*}$

     ATTENTION : $0,75 < 1$, donc $\ln(0,75) < 0$ ; quand on multiplie (divise) une inégalité par un négatif l'odre change !

     Donc $0,75^n > 0,25 \Leftrightarrow x \in \intoo{\dfrac{\ln(0,25)}{\ln(0,75)}}{+\infty}$

   •  

     $\begin{align*} & \e^{x + 2} > 4 \\ \Leftrightarrow & \ln \left( \e^{x + 2} \right) > \ln(4) \\ \Leftrightarrow & (x + 2) \ln(\e) > \ln(4) \\ \Leftrightarrow & (x + 2) \times 1 > \ln(4) \\ \Leftrightarrow & x > \ln(4) - 2\\ \end{align*}$

     Donc $\e^{x + 2} > 4 \Leftrightarrow x \in \intoo{-\infty}{\ln(4)-2}$

2. • $10 \log \left( \dfrac{i}{10^{-12}} \right) > 120 $
   • $20 \log \left( \dfrac{p}{2 \times 10^{-5}} \right) < 20 $
   • $7 = -\log(c)$
   • $10^x > 5$
   Solution

   •  

     $\begin{align*} & 10 \log \left( \dfrac{i}{10^{-12}} \right) > 120 \\ \Leftrightarrow & \log \left( \dfrac{i}{10^{-12}} \right) > 12 \\ \Leftrightarrow & \dfrac{i}{10^{-12}} > 10^{12}\\ \Leftrightarrow & i > 10^{12} \times 10^{-12}\\ \Leftrightarrow & i > 1 \end{align*}$

     Donc $10 \log \left( \dfrac{i}{10^{-12}} \right) > 120 \Leftrightarrow i \in \intoo{1}{+\infty}$

   •  

     $\begin{align*} & 20 \log \left( \dfrac{p}{2 \times 10^{-5}} \right) < 20 \\ \Leftrightarrow & \log \left( \dfrac{p}{2 \times 10^{-5}} \right) < 1 \\ \Leftrightarrow & \dfrac{p}{2 \times 10^{-5}} < 10 \\ \Leftrightarrow & p < 10 \times 2 \times 10^{-5}\\ \Leftrightarrow & p < 2 \times 10^{-4} \end{align*}$

     Donc $20 \log \left( \dfrac{p}{2 \times 10^{-5}} \right) < 20 \Leftrightarrow p \in \intoo{0}{2 \times 10^{-4}}$

   •  

     $\begin{align*} & 7 = -\log(c) \\ \Leftrightarrow & -7 = \log(c) \\ \Leftrightarrow & c = 10^{-7} \\ \end{align*}$

   •  

     $\begin{align*} & 10^x > 5 \\ \Leftrightarrow & \log(10^x) > \log(5) \\ \Leftrightarrow & x \log(10) > \log(5) \\ \Leftrightarrow & x > \log(5) \\ \end{align*}$

     donc $10^x > 5 \Leftrightarrow x \in \intoo{\log(5)} {+\infty}$.

     Remarque : en utilisant le logarithme népérien :

     $\begin{align*} & 10^x > 5 \\ \Leftrightarrow & \ln(10^x) > \ln(5) \\ \Leftrightarrow & x \ln(10) > \ln(5) \\ \Leftrightarrow & x > \dfrac{\ln(5)}{\ln(10)} \\ \end{align*}$

     puis (mais c'est inutilement compliqué) : $\dfrac{\ln(5)}{\ln(10)} = \dfrac{\ln\left(10^{\log(5)}\right)}{\ln(10)} = \dfrac{\log(5) \times \ln(10)}{\ln(10)} = \log(5)$

3. • $1,05^x > 10$
   • $\log(x) < 9,5$
   • $\e^{3 - x} < 10$
   • $\ln(3 + x) > 10$

   On considère les inéquations de la dernière série. Parmi les quatre intervalles solutions, l'un deux a une borne de la forme $\dfrac{a \ln(10)}{b}$ et un autre a une borne de la forme $c + d \ln(10)$. Clique ici pour écrire la valeur de $a + d$.

Problèmes

Alcoolémie

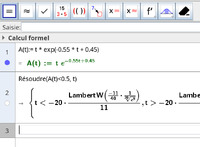
1. L'alcoolémie est le taux d'alcool dans le sang, il se mesure en $\text{g}\cdot\text{L}^{-1}$. On modélise l'alcoolémie en fonction du temps $t$ (en heure) écoulé depuis l'absorption de l'alcool par la fonction $A(t) = t \e^{- 0,55 t + 0,45}$

   1. Calculer l'alcoolémie (au centième) une heure et demi, puis trois heures vingt minutes après l'absorption.
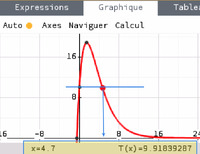
   2. Représenter la fonction $A$ à l'aide d'un logiciel et donner son sens de variation sur $\intfo0{+\infty}$.
   3. À l'aide du graphique, donner le temps nécessaire pour l'alcoolémie redevienne inférieure à $0,5 \text{g}\cdot\text{L}^{-1}$.
   4. Retrouver ce résultat à l'aide d'un logiciel de calcul formel.
   Aide

   1. une heure et demi, c'est $1,5$ heure ; donc $t=1,5$.
   2. calculatrice ou logiciel, mais souvent la variable doit être $x$ au lieu de $t$.
   3. légender les axes !

   4. GeoGebra possède une fenêtre Calcul formel.

      

      ligne 1 : affectation avec := et écrire tous les signes d'opération.

      ligne 2 : préciser la variable. Si le bouton = est sélectionné, les valeurs exactes ne sont pas toujours explicites ! Sélectionner le bouton ≈.

      Le séparateur décimal est le point.

   Solution

   1. une heure et demi, donc $t = 1,5$

      $A(1,5) = 1,5 \times \e^{-0,55 \times 1,5 + 0,45} \approx 1,03$

      Au bout d'une heure et demi, le taux d'alcoolémie est de $1,03 \text{g}\cdot\text{L}^{-1}$.

      trois heure vingt, donc $t = 3 + \dfrac13 = \dfrac{10}3$

      $A\left(\dfrac{10}3 \right) = \dfrac{10}3 \times \e^{-0,55 \times \frac{10}3 + 0,45} \approx 0,84$

      Au bout de trois heures vingt minutes, le taux d'alcoolémie est de $0,84 \text{g}\cdot\text{L}^{-1}$.

   2. 

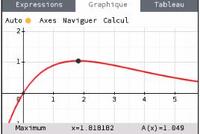
      La fonction est croissante sur $\intff{0}{1,82}$ puis décroissante sur $\intfo{1,82}{+\infty}$.

   3. 

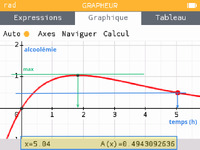
      par lecture graphique, il faut attendre environ 5 heures pour que l'alcoolémie soit à $0,5 \text{g}\cdot\text{L}^{-1}$.

Réaction chimique

1. La température $T$ (en degrés Celcius) d'une réaction chimique à l'instant $t$ (en minutes) est donnée par $T(t) = (20 t + 10)\e^{-0,5 t}$.

   1. Calculer la température initiale.
   2. Représenter la fonction $T$ à l'aide d'un logiciel et donner son sens de variation sur $\intfo0{+\infty}$.

   3. Un logiciel de calcul formel permet d'obtenir la forme factorisée de la dérivée de $T$. Retrouver par le calcul la valeur exacte du maximum de $T$.

      

   4. À l'aide du graphique, déterminer le temps nécessaire pour que la température retrouve sa valeur initiale.
   5. Retrouver ce résultat à l'aide d'un logiciel de calcul formel.
   Aide

   1. la mesure de la température commence pour $t=0$.
   2. calculatrice ou logiciel, mais souvent la variable doit être $x$ au lieu de $t$.
   3. • le maximum est atteint pour la valeur de $t$ qui annule la dérivée.
      • quelque soit $y \in \setR : \e^y > 0$
   4. légender les axes !
   Solution

   1. pour $t = 0$ on a $T(0) = (20 \times 0 + 10)\e^{-0,5 \times 0} = 10 \e^0 = 10$

      La température initiale de la réaction est $10^\circ C$

   2. 

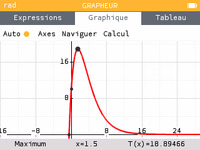
      La fonction est croissante sur $\intff{0}{1,5}$ puis décroissante sur $\intfo{1,5}{+\infty}$.

   3. On cherche $t$ tel que $T'(t) = 0$

      $\begin{align*} & T'(t)= 0 \\ \Leftrightarrow & -5 \e^{-\frac12 t} \times (2t - 3) = 0 \\ \Leftrightarrow & 2t - 3 = 0 \\ \Leftrightarrow & t = \dfrac32 \end{align*}$

      donc le maximum est $T\left( \frac32 \right) = (20 \times \dfrac32 + 10)\e^{-0,5 \times \frac32} = 40 \e^{-\frac34} \approx 18,89$.

   4. 

      La température revient à sa valeur initiale au bout de $4,7$ minutes.

   5. À l'aide d'un logiciel $T(t) = 10 \Leftrightarrow t \approx 4,67$, donc au bout de $4,67$ minutes.

Modélisation 1

1. Une étude vise à quantifier la probabilité $y_i$, pour une personne donnée, de développer une maladie après la consommation d'une portion de repas à base d'œuf ou de poulet selon le nombre $n_i$ de bactéries Salmonella qui y sont présentes.

   Les résultats de cette étude sont donnés dans le tableau suivant :

   $\begin{array}{l*{8}c} \hline n_i & 15 & 50 & 400 & \np{6300} & \np{2,5}\cdot 10^4 & \np{6,3}\cdot10^5 & 2\cdot10^6 & 4\cdot10^8 \\ \hline y_i & \np{0,02} & \np{0,15} & \np{0,27} & \np{0,63} & \np{0,71} & \np{0,84} & \np{0,92} & 1 \\ \hline \end{array}$

   Source: Organisation des Nations Unies pour l'alimentation et l'agriculture

   1. Écrire ces données dans une feuille de tableur.
   2. Construire le nuage de points associé à ces données. (le graphique doit s'adapter si on change une des valeurs !)
   3. Un ajustement affine est-il pertinent ? Justifier.
   Aide

   1. Afin d'exploiter au mieux la feuille de données, il faut écrire les données en colonnes et préciser le titre de chaque colonne.
   2. Utiliser une représentation type « nuage de points »
   3. Un ajustement affine implique que les points sont globalement alignés.

   On pose $x_i = \log \left(n_i\right)$.

   4. Compléter la feuille tableur en utilisant la fonction LOG ou LOG10 (à vérifier suivant les tableurs ; de plus les calculs doivent faire référence aux valeur de la colonne contenant les valeurs $n$ !) et afficher les résultats avec deux décimales.
   5. Construire un graphique type « nuage de points » qui met en relation les valeurs de $x$ et celles de $y$ (attention à l'ordre des données !).
   6. Justifier que dans ce cas un ajustement affine est pertinent et donner l'équation de la droite de régression avec des coefficients arrondis à $10^{-3}$.
   7. En utilisant ce modèle d'ajustement, estimer, à $10^{-2}$ près, la probabilité de développer une maladie après la consommation d'une portion de repas à base d'œuf ou de poulet dans lesquels le nombre de bactéries Salmonella est de $\np{4000}$.
   Aide

   1. Afin d'exploiter au mieux la feuille de données, il faut écrire les données en colonnes et préciser le titre de chaque colonne.
   2. Utiliser une représentation type « nuage de points »
   3. Par défaut, le tableur prend la colonne la plus à droite pour les abscisses : la fenêtre de dialogue permet de changer ce comportement.
   4. Un ajustement affine implique que les points sont globalement alignés.
   Solution

   6. la droite de régression a pour équation $y = \np{0,141} x - \np{0,038}$
   7. $n=\np{4000}$, donc $x=\log(\np{4000})$ et $y = \dots$

   Pour la suite, on utilise un nouveau modèle d'ajustement.

   Pour un nombre $n$ de bactéries donné, on pose $x = \log(n)$ et, dans ce nouveau modèle, on note $p(x)$ la probabilité, pour une personne donnée, de développer une maladie après la consommation d'une portion de repas à base d'œuf ou de poulet selon le nombre $n$ de bactéries Salmonella qui y sont présentes.

   On suppose que pour tout $x \in \intfo0{+\infty}$, on a : $p(x) = \dfrac{1}{1 + \np{34,8}\text{e}^{- x}}$.

   8. Compléter la feuille de tableur et tracer la fonction $p$ dans le graphique (relier les points entre eux).
   9. À l'aide d'une lecture graphique, déterminer le sens de variation de $p$, puis le signe de $p'$ (fonction dérivée de $p$).
   Aide

   9. Si la fonction dérivée est positive, alors la fonction étudiée est croissante.
   10. Déterminer l'expression de $p'(x)$ à l'aide d'un logiciel de calcul formel.
   11. Déterminer (en justifiant) le signe de $p'(x)$ sur $\intfo0{+\infty}$.
   solution

   10. GeoGegra donne : $p'(x) = 870 \times \ffrac{\e^{-x}}{(174 \e^{-x} + 5)^2}$
   11. • Quelque soit le réel $a$ : $\e^a > 0$
       • dénominateur : quelque soit $x \in \intfo0{+\infty} \,; \e^{-x} > 0 \Leftrightarrow 870 \e^{-x} > 0$ (multiplication par un positif : l'ordre est conservé).
       • le dénominateur est un carré, donc toujours positif
       • $p'(x)$ est le quotient de deux expressions strictement positives : donc $p'(x) > 0$.
   12. En utilisant ce nouveau modèle, déterminer la probabilité de développer une maladie après la consommation d'une portion de repas à base d'œuf ou de poulet dans lesquels le nombre de bactéries Salmonella est de $\np{4000}$ (arrondir au centième).
   13. En utilisant ce nouveau modèle, estimer le nombre de bactéries Salmonella d'une portion de repas à base d'œuf ou de poulet telle que la probabilité d'être malade soit égale à $\np{0,75}$. (Expliquer la démarche utilisée).
   Aide

   12. $n = \np{4000}$, donc $x = \log{\np{4000}}$ et $p(x) = \dots$
   13. on cherche $x$ tel que $p(x) = \np{0,75}$ ; puis on cherche $n$ sachant que $x = \log(n)$.

Modélisation 2

1. On étudie la croissance d'une population de crustacés planctoniques dans un environnement limité.

   On note $x$ le nombre des individus de cette population à l'instant $t$ exprimé en jours. Les résultats obtenus sont dans le tableau suivant :

   $\begin{array}{l*9c} \hline t_{i} \text{(en jours)} &0 &2 &4 &6 &8 &10 &12 &14\\ \hline x_{i} \text{(effectif)} &15&59 &199 &448 &631 &697 &715 &719\\ \hline \end{array}$

   1. Écire ces données dans une feuille de tableur.
   2. Construire le nuage de points associé à ces données. (le graphique doit s'adapter si on change une des valeurs !)
   3. Un ajustement affine est-il pertinent ? Justifier.
   Aide

   1. Afin d'exploiter au mieux la feuille de données, il faut écrire les données en colonnes et préciser le titre de chaque colonne.
   2. Utiliser une représentation type « nuage de points »
   3. Un ajustement affine implique que les points sont globalement alignés.

   On pose $y = \ln \left(\dfrac{x}{720 - x}\right)$.

   4. Compléter la feuille tableur en utilisant la fonction LN (les calculs doivent faire référence aux valeur de la colonne contenant les valeurs $x$ !) et afficher les résultats avec deux décimales.
   5. Construire un graphique type « nuage de points » qui met en relation les valeurs de $t$ et celles de $y$.
   6. Justifier que dans ce cas un ajustement affine est pertinent et donner l'équation de la droite de régression avec des coefficients arrondis à $10^{-2}$.
   Aide

   • Si la première valeur de la colonne contenant les valeurs de $x$ est en cellule B5 il est judicieux que la première valeur de colonne de $y$ soit en C5 et d'y écrire la formule du type =LN(B5) qui pourra être copiée -collée vers le bas.
   • Pour sélectionner deux plages discontinues, on peut utiliser la touche Ctrl tout en surlignant à l'aide de la souris.

   4. pour $x=0$, il faut trouver $y=\np{-3,85}$
   6. plus le paramètre $R^2$ est proche de $1$, plus l'ajustement affine est pertinent.
   Solution

   6. on trouve $y = \np{0,74}t - \np{3,91}$
   7. Montrer que $x = \dfrac{720}{1 + \e^{-\np{0,74}t + \np{3,91}}}$ ce qui détermine $x$ comme fonction de $t$ sur $\intfo0{+ \infty}$.

   8. Calculer $\displaystyle\lim_{t \to + \infty} x(t)$, puis interpréter ce résultat dans le contexte de l'exercice.

      Ce résultat est-il cohérent avec la réalité expérimentale ?

   Aide

   7. On sait que $y = \np{0,74}t - \np{3,91}$ et $y = \ln \left(\dfrac{x}{720 - x}\right)$ donc $\ln \left(\dfrac{x}{720 - x}\right)= \np{0,74}t - \np{3,91}$

      quelque soit le réel $a$ : $\e^a \times \e^{-a} = 1$

   8. Remarque : le fait de changer l'expression permet de « lever l'indétermination » dans le calcul de la limite