Variables aléatories continues - loi normale
De la loi binomiale à la loi normale
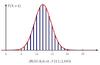
Chaque gaphique représente une loi binomiale (diagramme en bâtons) et la loi normale assoicée (courbe de la fonction).
-
Reproduire chacune de ces lois à l'aide de la calculatrice
-
-
À retenir :
La loi binomiale peut être approximée par la loi normale :
- cela permet de travailler sur des variables aléatoires continues ;
- avant l'informatique, cela simplifiait les calculs.
-
La Direction de la recherche, des études, de l'évaluation et des statistiques (Drees) affirme qu'en France $7$ adultes sur $10$ portent des lunettes.
On prélève au hasard un échantillon de $40$ adultes parmi la population française. On assimile ce prélèvement à un tirage avec remise.
Soit $X$ la variable aléatoire qui, à tout échantillon de ce type, associe le nombre de porteurs de lunettes dans l'échantillon.
-
Montrer que $X$ suit une loi binomiale dont on précisera les paramètres.AideLa loi binomiale a pour paramètres $n$ et $p$ ; $n$ est la taille de l'échantillon et $p$ la probabilité de porter des lunettes.
-
Calculer la probabilité qu'il y ait au moins $30$ porteurs de lunettes dans un tel échantillon de $40$ adultes. On donnera la valeur arrondie à $10^{-3}$.Aide« au moins $30$», donc on veut $X \geqslant 30$.
-
On admet que la loi binomiale de la variable aléatoire $X$ précédente peut être approchée par une loi normale de paramètres $\mu$ et $\sigma$.
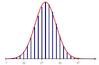
On a représenté ci-dessous un diagramme en bâtons représentant la loi binomiale suivie par $X$ et une courbe $\mathscr C$ représentant la loi normale associée de paramètres $\mu$ et $\sigma$.
La courbe représentant la loi normale est symétrique par rapport à la droite d'équation $x=\mu$. Donner, par lecture graphique, la valeur de $\mu$.
-
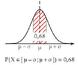
On sait que pour toute loi normale de paramètres $(\mu\,; \sigma)$, $p( X \in \intff{\mu - \sigma}{\mu + \sigma}) \approx \np{0,68}$.
Arnufle affirme que l'écart type $\sigma$ de cette loi normale est égal à $8$. Que penser de cette affirmation ?
-
- la représentation de la loi normale est une courbe en cloche
- la courbe est symétrique axiale par rapport à $x = \mu$
- la surface hachurée représente la probabilité :
-
- l'aire totale sous la courbe vaut $1$.
-
Une personne est dite en hypoglycémie si sa glycémie à jeun est inférieure à $\np{60}\text{mg }\cdot \text{dL}^{-1}$ et elle est en hyperglycémie si sa glycémie à jeun est supérieure à $\np{110}\text{mg }\cdot \text{dL}^{-1}$. La glycémie à jeun est considérée comme normale si elle est comprise entre $\np{70}\text{mg }\cdot \text{dL}^{-1}$ et $\np{110}\text{mg }\cdot \text{dL}^{-1}$. Les personnes ayant un taux de glycémie compris entre $60$ et $\np{70}\text{mg }\cdot \text{dL}^{-1}$ ne font pas l'objet d'un suivi particulier.
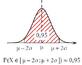
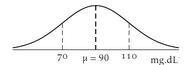
On modélise la glycémie à jeun, exprimée en $\text{mg}\cdot\text{dL}^{-1}$, d'un adulte d'une population donnée, par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 90$ et d'écart-type $\sigma = \np{12,3}$.
On donne ci-dessous la représentation graphique de la densité de probabilité de la variable aléatoire $X$.
-
Quelle est la probabilité que la personne choisie ait une glycémie à jeun «normale» ?
-
Calculer la probabilité que la personne choisie soit en hyperglycémie.
-
Calculer la probabilité que la personne choisie soit en hypoglycémie.
-
À retenir :
La loi normale $\mathscr N(\mu\,; \sigma)$ est une approximation de la loi binomiale $\mathscr B(n\,;p)$ avec $np > 1$.
La représentation de la loi normale est une courbe en cloche. On a toujours :
