Exercices : Probabilités
Probabilités discrètes
Défauts de fabrication et conformité
L'entreprise AGOREX fabrique et distribue des pipettes jaugées en verre. Deux chaînes de production (A et B) permettent de répondre à la demande journalière.- 55 % des pipettes viennent de la chaîne de production A et 2,6 % des pipettes de cette chaîne sont inutilisables ;
- 3,6 % des pipettes provenant de la chaîne de production B sont inutilisables.
On choisit au hasard une pipette dans le stock journalier de l'entreprise et on note :
- $A$ l'événement : «La pipette est sortie de la chaîne de production A» ;
- $B$ l'événement : «La pipette est sortie de la chaîne de production B» ;
- $I$ l'événement : «La pipette est inutilisable»
-
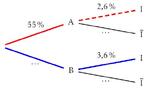
Représenter cette situation l'aide d'un arbre de probabilités.Aide
Rappels :
- arbre : racine, branche, nœud, feuille, chemin.
- la probabilité de l'événement $A$ est $p(A) = 0,55$.
- probabilité conditionnelle : la probabilité de l'événement $I$ sachant que l'événement $A$ est réalisé est $p_A(I) = 2,6\,\% = 0,026$ (c'est la branche en pointillés rouges)
- événement contraire : l'événément contraire de $I$ se note $\overline{I}$.
- la somme des probabilités des branches issues d'un même nœud vaut toujours $1$, donc $p(I) + p(\overline{I}) = 1 \ssi p(\overline{I}) = 1 - p(I)$.
- probabilité suivant un chemin : le chemin représenté par les branches rouges, correspond à l'événement $A \text{ et } I$, on le note $A \cap I$ et sa probabilité est $p(A \cap I) = p(A) \times p_A(I) \ssi p_A(I) = \dfrac{p(A \cap I)}{p(A)}$
- probabilités totales : Pour trouver la probabilité de l'événement $I$, on peut suivre le chemin rouge OU le chemin bleu ; donc $p(I)= {\color{red}{p(A \cap I)}} + {\color{blue}{p(\overline A \cap I)}}$ (c'est la formule des probabilités totales)
- événements indépendants : Deux événéments $A$ et $I$ sont indépendants si et seulement si $p(A \cap I) = p(A) \times p(I)$ ; autrement dit si et seulement si $p_A(I) = p(I)$ : la réalisation de $A$ n'influe pas celle de $I$.
- la réalisation de l'événement $A \text{ ou } I$ se note $A \cup I$ et sa probabilité est $p(A \cup I) = p(A) + p(I) - p(A \cap I)$.
- Le «OU» Augmente les chances de réussite : on Addtionne les probabilités.
- Le «ET» réduit les chances de réussite : on multiplie les probabilités.
-
Calculer à $10^{-3}$ près la probabilité qu'une pipette soit inutilisable.Aide
On cherche à calculer $p(I)$.
D'après l'arbre, on arrive à $I$ en passant par le chemin rouge OU le chemin bleu ; donc $p(I) = p(A \cap I) + p(B \cap I)$
-
On suppose que la probabilité (arrondie au centième) qu'une pipette soit inutilisable est égale à $0,03$.
On prélève au hasard un échantillon de 100 pipettes dans le stock de l'entreprise. Le nombre de pipettes produites est suffisamment important pour que l'on assimile ce prélèvement à un tirage avec remise de 100 pipettes.
On considère la variable aléatoire $X$ qui, à tout prélèvement de 100 pipettes, associe le nombre de pipettes inutilisables.
- Déterminer la loi suivie par $X$ en précisant ses paramètres.
- Quelle est la probabilité de l'événement : «au moins une des pipettes est inutilisable» ? On arrondira cette probabilité au millième.
Aide (a)Une épreuve de Bernoulli de paramètre $p$ est une expérience aléatoire qui n'a que deux issues : Succès ($S$) et Echec($E$) telle que la probabilité de $S$ soit $p$
Un schéma de Bernoulli de paramètres $n$ et $p$ est la répétition de façon identiques et indépendantes de $n$ épreuve de Bernoulli de paramètre $p$.
La variable aléatoire $X$ qui compte le nombre de succès dans un schéma de Bernoulli suit la loi binomiale de paramètres $n$ et $p$. On note $X \sim \mathscr B(n; p)$.
Aide (b)On calcule $p(x = k)$ à l'aide de la calculatrice.
Exemple :
- on lance exactement de la même façon, une pièce de monnaie parfaitement équilibrée 20 fois de suite et on compte le nombre de pile.
- Dans ce cas, la variable aléatoire $X$ qui compte le nombre de pile suit la loi binomiale de paramètres $n = 20$ et $p = 0,5$.
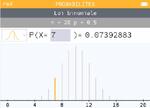
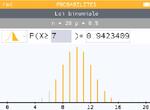
- la probabilité d'obtenir exactement $7$ pile dans la série de $20$ lancers est $p(X = 7) \simeq 0,074$ et celle d'obtenir au moins $7$ piles est $p(X \geqslant 7) \simeq 0,942$
-
 -
-
Embouteillage
Dans une usine, une machine à embouteiller est alimentée par un réservoir d'eau et par une file d'entrée qui permet l'approvisionnement en bouteilles vides.
On considère qu'il y a un défaut d'approvisionnement lorsqu'au moins un des deux cas suivants est réalisé:
- la file d'entrée des bouteilles est vide ;
- le réservoir est vide.
On choisit au hasard un jour d'activité de l'entreprise dans l'année. On note:
- $A$ l'évènement: «la file d'entrée des bouteilles est vide au moins une fois dans la journée»;
- $B$ l'évènement: «le réservoir est vide au moins une fois dans la journée».
On admet que les évènements $A$ et $B$ sont indépendants.
Une étude statistique permet de dire que les probabilités des évènements $A$ et $B$ sont respectivement données par $P(A) = 0,03$ et $P(B) = 0,02$.
-
Chaque phrase du tableau du haut est associée à une unique information correspondante dans le tableau du bas.
Donner en jusitifiant le numéro de la phrase avec la lettre qui correspond à l'information associée.
1 La probabilité de l'évènement: «La file d'entrée ne se vide pas dans la journée.» 2 L'évènement : «La file d'entrée est vide au moins une fois dans la journée mais pas le réservoir.» 3 La probabilité de l'évènement : «La file d'entrée et le réservoir ont été tous les deux vides au moins une fois au cours de la journée.» 4 La probabilité de l'évènement : «La machine a connu un défaut d'approvisionnement dans la journée. » A $\overline{A} \cap B$ B $0,05$ C $A \cap \overline{B}$ D $\np{0,0494}$ E $\np{0,97}$ F $\np{0,0006}$ -
Lorsque la machine tombe en panne, elle est immobilisée pour le reste de la journée et réparée pour le lendemain.
La probabilité qu'elle tombe en panne un jour quelconque est égale à $0,025$.
On note $X$ la variable aléatoire qui, à toute période de $200$ jours consécutifs choisie au hasard, associe le nombre de jours où la machine est tombée en panne.
On considère que les jours où les pannes surviennent sont indépendants les uns des autres.
- Donner, sans justifier, la loi de probabilité suivie par la variable aléatoire $X$. Préciser ses paramètres.
- En déduire la valeur à $10^{-3}$ de la probabilité $p(X \leqslant 10)$ et interpréter dans le contexte.