Frédéric Léon -- MATHS -- E. Brontë

▲

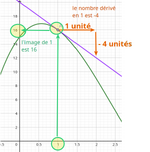
Nombre dérivé

p. 88 n° 57

  1. Nous avons généralisé la question 1 :

    Si $f(x) = mx + p$, alors quelque soit le réel $a$ : $f'(a) = m$.

  2. $f(x) = 5x^2 - 3x + 2$ : calculer le nombre dérivé en $a=-1$

    Aide

    Suivre le plan de travail

    1. Exprimer le plus simplement possible le taux d'accroissement : $\tau(h) = \ffrac{ f(a + h) - f(a)}h$
    2. Calculer la limite quand $h$ tend vers $0$ de $\tau(h)$.
    3. Si cette limite est un réel, alors c'est le nombre dérivé et on a $\lim\limits_{h \to 0}\tau(h) = f'(a)$
    Solution

    1. $\begin{align*} & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \Leftrightarrow & \tau(h) = \ffrac{ f(-1 + h) - f(-1)}h \\ \end{align*}$

      $\begin{align*} f(-1+h) & = 5(-1 + h)^2 - 3(-1 + h) + 2 \\ & = 5(1 - 2h + h^2) + 3 - 3h + 2 \\ & = 10 - 13 h + 5 h^2 \end{align*}$

      $f(-1) = 10$

      donc $\tau(h) = \ffrac{-13 h + 5h^2}h = -13 + 5 h$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{-13 + 5 \times 0 = -13}$ ; donc $\lim\limits_{h \to 0}\tau(h) =-13$
    3. on en déduit que $f'(-1) = -13$

  3. Pour prolonger : $f(x) = 5x^2 - 3x + 2$ : calculer le nombre dérivé en $a$

    Solution

    1. $\tau(h) = \ffrac{ f(a + h) - f(a)}h$

      $\begin{align*} f(a+h) & = 5(a + h)^2 - 3(a + h) + 2 \\ & = 5(a^2 + 2ah + h^2) - 3a - 3h + 2 \\ & = 5a^2 + 10ah + 5 h^2 - 3a -3h +2 \\ & = \color{red}{5a^2} + 10ah + 5 h^2 \color{red}{- 3a} -3h \color{red}{+2} \\ & = \color{red}{f(a)} + 10 ah - 3 h + 5 h^2 \end{align*}$

      une astuce de calcul pour éviter des calculs ;-) : faire apparaître $f(a)$

      donc $f(a+h) - f(a) = 10ah - 3h + 5h^2$

      d'où $\tau(h) = 10a - 3 + 5 h$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{10a -3 + 5 \times 0 = 10a - 3}$ ; donc $\lim\limits_{h \to 0}\tau(h) =10a - 3$
    3. on en déduit que $f'(a) = 10a - 3$
    4. remarque : pour $a = -1$, on retrouve bien $f'(-1) = 10 \times(-1) -3 = -13$

p. 88 n° 59

  1. $f(x) = \ffrac3x$ : calculer le nombre dérivé en $a=1$

    Aide

    Suivre le plan de travail

    1. Exprimer le plus simplement possible le taux d'accroissement : $\tau(h) = \ffrac{ f(a + h) - f(a)}h$
    2. Calculer la limite quand $h$ tend vers $0$ de $\tau(h)$.
    3. Si cette limite est un réel, alors c'est le nombre dérivé et on a $\lim\limits_{h \to 0}\tau(h) = f'(a)$
    Solution

    1. $\begin{align*} & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \Leftrightarrow & \tau(h) = \ffrac{ f(1 + h) - f(1)}h \\ \end{align*}$

      $f(1+h) = \ffrac{3}{1 + h}$

      $f(1) = 3$

      donc

      $\begin{align*} & \tau(h) = \ffrac{\ffrac{3}{1 + h} - 3}h\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( \ffrac{3}{1 + h} - \ffrac{3 (1+h)}{1+h} \right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( \ffrac{3 - 3 - 3h}{1 + h} \right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \times \ffrac{- 3h}{1 + h} \\ \Leftrightarrow & \tau(h) = \ffrac{- 3}{1 + h} \end{align*}$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{\ffrac{-3}{1 + 0} = -3}$ ; donc $\lim\limits_{h \to 0}\tau(h) =-3$
    3. on en déduit que $f'(1) = -3$

  2. pour prolonger : $f(x) = \ffrac3x$ : calculer le nombre dérivé en $a$ $(a \neq 0)$

    Solution

    1. $\begin{align*} & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \Leftrightarrow & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \end{align*}$

      $f(a+h) = \ffrac{3}{a + h}$

      $f(a) = \ffrac3a$

      donc

      $\begin{align*} & \tau(h) = \ffrac{\ffrac{3}{a + h} - \ffrac3a}h\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( \ffrac{3 \times a}{(a + h)\times a} - \ffrac{3 (a+h)}{a \times (a+h)} \right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( \ffrac{3a - 3a - 3h}{a(a + h)} \right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \times \ffrac{- 3h}{a(a + h)} \\ \Leftrightarrow & \tau(h) = \ffrac{- 3}{a(a + h)} \end{align*}$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{\ffrac{-3}{a(a +0)} = \ffrac{-3}{a^2}}$ ; donc $\lim\limits_{h \to 0}\tau(h) =\ffrac{-3}{a^2}$
    3. on en déduit que $f'(a) = \ffrac{-3}{a^2}$

  3. $f(x) = x + \ffrac1x$ : calculer le nombre dérivé en $a=-1$

    Solution

    1. $\begin{align*} & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \Leftrightarrow & \tau(h) = \ffrac{ f(-1 + h) - f(-1)}h \\ \end{align*}$

      $f(-1+h) = (-1 + h) + \ffrac{1}{-1 + h}$

      $f(-1) = -2$

      donc

      $\begin{align*} & \tau(h) = \ffrac{(-1 + h) + \ffrac{1}{-1 + h} - (-2)}h\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( (1 + h) + \ffrac{1}{-1 + h}\right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \times \ffrac{(1+h)(-1+h) + 1}{-1 + h}\\ \Leftrightarrow & \tau(h) = \ffrac1h \times \ffrac{h^2}{-1+h}\\ \Leftrightarrow & \tau(h) = \ffrac{h}{1 + h} \end{align*}$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{\ffrac{0}{1 + 0} = 0}$ ; donc $\lim\limits_{h \to 0}\tau(h) =0$
    3. on en déduit que $f'(-1) = 0$

  4. pour continuer : $f(x) = x + \ffrac1x$ : calculer le nombre dérivé en $a$

    Solution

    1. $\begin{align*} & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \Leftrightarrow & \tau(h) = \ffrac{ f(a + h) - f(a)}h \\ \end{align*}$

      $f(a+h) = (a + h) + \ffrac{1}{a + h}$

      $f(a) = a + \ffrac1a$

      donc

      $\begin{align*} & \tau(h) = \ffrac{(a + h) + \ffrac{1}{a + h} - \left( a + \ffrac1a\right)}h\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( h + \ffrac{1}{a + h} - \ffrac1a\right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( h + \ffrac{a}{a(a + h)} - \ffrac{a + h}{a(a+h)}\right)\\ \Leftrightarrow & \tau(h) = \ffrac1h \left( h - \ffrac{h}{a(a + h)} \right)\\ \Leftrightarrow & \tau(h) = 1 - \ffrac{1}{a(a + h)} \end{align*}$

    2. Quand $h$ tends vers $0$, $\tau(h)$ est de la forme $\color{blue}{1 - \ffrac{1}{a(a + 0)} = 1 - \ffrac1{a^2}}$ ; donc $\lim\limits_{h \to 0}\tau(h) =1 - \ffrac1{a^2}$
    3. on en déduit que $f'(a) = 1 - \ffrac1{a^2}$

p. 86 n° 41

  1. Déterminer par lecture graphique :

    1. $f(-2)$ puis $f'(-2)$
    2. $f(-1)$ puis $f'(-1)$
    3. $f(0)$ puis $f'(0)$
    4. $f(1)$ puis $f'(1)$
    Aide
    • $f(a)$ est l'image de $a$ par la fonction $f$
    • $f'(a)$ est la pente de la tangente au point d'abscisse $a$
    lire image / lire nb dérivé
    Solution
    1. $f(-2)=4$ et $f'(-2)=0$
    2. $f(-1)=3$ et $f'(-1)=-2$
    3. $f(0)=2$ et $f'(0)=0$
    4. $f(1)=3$ et $f'(1)=2$

  2. Déterminer l'équation réduite des tangentes.

    Aide

    Voir cours du 15/11/25 : l'équation réduite de la droite $(AB)$ est : $y = \ffrac{y_B - y_A}{x_B - x_A}(x - x_A) + y_A$

    on sait que le coefficient directeur de la tangente est $f'(x_A)$ et que $y_A = f(x_A)$ ; on en déduit l'équation réduite de la tangente :

    $y = f'(x_A)(x - x_A) + f(x_A)$

    Solution
    1. pour le point A : $x_A = -2$ donc $y = f'(-2) (x - (-2)) + f(-2) \Leftrightarrow y = 4$
    2. pour le point B : $x_B = -1$ donc $y = f'(-1) (x - (-1)) + f(-1) \Leftrightarrow y = -2 x + 1$
    3. pour le point C : $x_C = 0$ donc $y = f'(0) (x - 0) + f(0) \Leftrightarrow y = 2$
    4. pour le point D : $x_D = 1$ donc $y = f'(1) (x - 1) + f(1) \Leftrightarrow y = 2 x + 1$

p. 90 n° 74

  1. $\mathscr D : y = -2x+3$ est tangente à la courbe de $f$ au point $A$ d'abscisse $3$.

    Déterminer $f'(3)$ et les coordonnées du point $A$.

    Aide
    • Le nombre dérivé est le coefficient directeur de la tangente.
    • Si un point appartient à une courbe, ses coordonnées vérifient l'équation.
    Solution

    $f'(3) = -2$

    le point $A$ appartient à la tangente, donc $f(3) = y_A = -2 \times 3 + 3 = -3$

p. 90 n° 75

  1. $\mathscr D : y = 5x - 2$ est tangente à la courbe de $f$ au point $A$ d'abscisse $-1$.

    Déterminer $f'(-1)$ et les coordonnées du point $A$.

    Solution

    $f'(-1) = 5$

    le point $A$ appartient à la tangente, donc $f(-1) = y_A = 5 \times (-1) - 2 = -7$