Exercices : Fonctions trigonométriques
- p.213 nº 2
- p.213 nº 3
- p.213 nº 4
- p.222 nº 39
- p.223 nº 48
- p.225 nº 68
- p.226 nº 80
- p.226 nº 71
- p.228 nº 94
- p.230 nº 106
- p.230 nº 107
- p.227 nº 89
p.213 nº 2
réels associés à un point
Placer les points associés aux réels :
| point | R | S | T | U | V |
|---|---|---|---|---|---|
| réels | $\dfrac{2\pi}3$ | $\dfrac{13\pi}6$ | $\dfrac{21\pi}4$ | $-\dfrac{19\pi}2$ | $-15\pi$ |
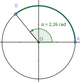
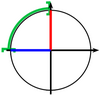
Le sens positif (le sens trigonométrique) est le sens contraire des aiguilles d'une montre
Dans le sens positif la mesure de l'angle en radian correspond à longueur de l'arc $\widearc{AB}$
Le cercle complet correspond à un angle de $2\pi$ radians.
Les multiples de $\dfrac{\pi}3$ ont pour cosinus $\pm\dfrac12$ ; les multiples de $\dfrac{\pi}6$ ont pour sinus $\pm\dfrac12$ ; les multiples de $\dfrac{\pi}4$ sont les bissectrices du repère.
p.213 nº 3
Montrer que les réels suivant sont associés au même point.
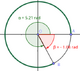
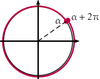
Deux réels $\alpha$ et $\beta$ sont sur le même point du cercle trigonométrique s'ils différent d'un multiple de $2\pi$.
Image mentale : partant de $\alpha$, il faut faire $k$ tours complets pour rejoindre $\beta$.
Mathématiquement : il existe un entier relatif $k$ tel que : $\beta = \alpha + k \times (2 \pi) \Leftrightarrow \beta - \alpha = k \times (2\pi) \Leftrightarrow \dfrac{\beta - \alpha}{2\pi} = k$
- $\dfrac{17\pi}4 - \dfrac{\pi}4 = \dfrac{16\pi}4 = 4\pi = \color{red}{2} \times (2\pi)$ ; donc en faisant $\color{red}{2}$ tours dans le sens trigonométrique en partant de $\dfrac{\pi}4$, on arrive sur le même point qui correspond à $\dfrac{17\pi}4$
- $-\dfrac{23\pi}4 - \dfrac{\pi}4 = -\dfrac{24\pi}4 = -6\pi = \color{red}{-3} \times (2\pi)$ ; donc en faisant $\color{red}{3}$ tours dans le sens inverse au sens trigonométrique en partant de $\dfrac{\pi}4$, on arrive sur le même point qui correspond à $-\dfrac{23\pi}4$
clique ici pour écrire le nombre de tours nécessaires pour atteidre $\dfrac{89\pi}4$ à partir de $\dfrac{17\pi}4$.
p.213 nº 4
Trouver l'intrus
-
a) $0$ ; b) $2\pi$ ; c) $-5\pi$ ; d) $-6\pi$ ;AideSolution
l'intrus est $-5\pi$ ; en effet $0$ est à la même position que $2\pi$, car $2\pi = \color{red}{1} \times 2\pi$ ; et que $-6\pi$, car $-6\pi = \color{red}{-3} \times 2\pi$.
-
a) $\dfrac{\pi}2$ ; b) $\dfrac{3\pi}2$ ; c) $-\dfrac{3\pi}2$ ; d) $\dfrac{5\pi}2$ ;
-
a) $\dfrac{3\pi}4$ ; b) $-\dfrac{5\pi}4$ ; c) $\dfrac{7\pi}4$ ; d) $\dfrac{11\pi}4$ ;
-
a) $\dfrac{\pi}3$ ; b) $-\dfrac{4\pi}3$ ; c) $-\dfrac{5\pi}3$ ; d) $\dfrac{7\pi}3$ ;
clique ici pour écrire les trois lettres des intrus pour les questions 2 à 4.
p.222 nº 39
Donner la valeur associée en radians
-
Valeurs dans $[0\,;2\pi[$.AideSolution
- $45^\circ$ est associé à $\dfrac{\pi}4$
- $150^\circ$ est associé à $\dfrac{5\pi}6$
- $60^\circ$ est associé à $\dfrac{5\pi}3$
-
Valeurs dans $[-\pi\,;\pi[$.Solution
- $45^\circ$ est associé à $\dfrac{\pi}4$
- $150^\circ$ est associé à $\dfrac{5\pi}6$
- $60^\circ$ est associé à $-\dfrac{\pi}3$
clique ici pour écrire l'angle en degrés associé à $-\dfrac{\pi}6$.
p.223 nº 48
- Si $x \in \intff0{\dfrac{\pi}2}$, alors $\sin x \geqslant 0$
- Si $\sin x \geqslant 0$, alors $x \in \intff0{\dfrac{\pi}2}$
- Si $x \in \intff0{\pi}$, alors $\cos x \geqslant 0$
- Si $\cos x \geqslant 0$, on peut avoir $x \in \intff{-\dfrac{\pi}2}{\dfrac{\pi}2}$
clique ici pour écrire les quatre lettres (en majuscule) V ou F (Vrai ou Faux) correspondant aux réponses.
p.225 nº 68
Calculer la valeur exacte de $\cos x$
-
Aide
- En utilisant la formule $\cos^2 x + \sin^2 x = 1$, on calcule la valeur exacte de $\cos^2 x$.
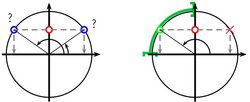
En utilisant un cercle trigonométrique, on peut déterminer le signe de $\cos x$
si on ne connaît que la valeur de $\color{red}{\sin x}$, il y a deux réels possibles ; mais si on sait que $\color{green}{x \in \left[ \dfrac{\pi}2\,; \pi \right[}$, alors un seul réel $x$ est possible et on connaît aussi son cosinus !
Solution$\cos^2 x + \sin^2 x = 1 \Leftrightarrow \cos^2 x = \dfrac{16}{25}$
$x \in \left[ 0 \,; \dfrac{\pi}2 \right]$, donc $\cos x \geqslant 0$
donc $\cos x = \dfrac45$.
-
Solution
$\cos^2 x + \sin^2 x = 1 \Leftrightarrow \cos^2 x = \dfrac{16}{25}$
$x \in \left[ \dfrac{\pi}2 \,; \pi \right]$, donc $\cos x \leqslant 0$
donc $\cos x = -\dfrac45$.
-
Solution
$\cos^2 x + \sin^2 x = 1 \Leftrightarrow \cos^2 x = \dfrac{21}{25}$
$x \in \left[ \dfrac{3\pi}2 \,; 2\pi \right]$, donc $\cos x \geqslant 0$
donc $\cos x = \dfrac{\sqrt{21}}5$.
Soit $x \in [-\pi \,; 0]$ et $\cos x = \dfrac{15}{17}$. clique ici pour écrire la valeur de $\sin x$ sous forme de fraction réduite (exemple : pour $-\dfrac68$ écrire «-3sur4»).
p.226 nº 80
-
Soit $a \in \intff0{\dfrac{\pi}2}$ tel que $\cos a = \dfrac35$.
Montrer que $\sin a = \dfrac45$.
Aide- En utilisant la formule $\cos^2 x + \sin^2 x = 1$, on calcule la valeur exacte de $\cos^2 x$.
En utilisant un cercle trigonométrique, on peut déterminer le signe de $\cos x$
si on ne connaît que la valeur de $\color{red}{\sin x}$, il y a deux réels possibles ; mais si on sait que $\color{green}{x \in \left[ \dfrac{\pi}2\,; \pi \right[}$, alors un seul réel $x$ est possible et on connaît aussi son cosinus !
Solution$\cos^2 a + \sin^2 a = 1 \Leftrightarrow \sin^2 a = \dfrac{16}{25}$
$a \in \left[ 0 \,; \dfrac{\pi}2 \right]$, donc $\sin a \geqslant 0$
donc $\sin a = \dfrac45$.
-
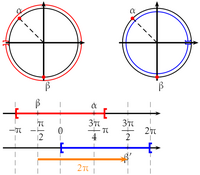
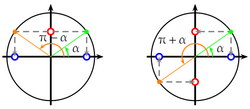
a) $\cos(-a)$ b) $\sin(-a)$ c) $\cos(\pi + a)$ d) $\sin(\pi + a)$ e) $\cos(\pi - a)$ f) $\sin(\pi - a)$ g) $\cos(a + 2\pi)$ h) $\sin(a + 2\pi)$ AideUtiliser la cercle trigonométrique et les symétries axiales et centrales
figure gauche figure droite $\color{blue}{\cos}(\color{brown}{\pi - \alpha}) = \color{blue}{-\cos}\color{green}{\alpha}$ $\color{blue}{\cos}(\color{brown}{\pi + \alpha}) = \color{blue}{-\cos}\color{green}{\alpha}$ $\color{red}{\sin}(\color{brown}{\pi - \alpha}) = \color{red}{\sin}\color{green}{\alpha}$ $\color{red}{\sin}(\color{brown}{\pi + \alpha}) = \color{red}{-\sin}\color{green}{\alpha}$
clique ici pour écrire dans l'ordre alphabétique les lettres minuscules des questions dont la réponse est $-\dfrac35$.
p.226 nº 71
- Calculer pour différents réels $x$ la valeur de l'expression $A(x) = (\cos x + \sin x)^2 + (\cos x - \sin x)^2$.
- Émettre une conjecture.
- Démontrer la conjecture
$A(x)$ est constante quelque soit $x$.
p.228 nº 94
-
Résoudre sur $[-\pi\,; \pi]$ : $\cos x \geqslant \dfrac12$.Aide
Tous les réels $x$ associés aux points de l'arc de cercle rouge vérifient $\cos x \geqslant \dfrac12$.
À l'aide du schéma déterminer les réels associés aux extrémités de l'arc de cercle rouge.
Solutionles réels de $[-\pi\,; \pi]$ ayant pour cosinus $\dfrac12$ sont $-\dfrac{\pi}3$ et $\dfrac{\pi}3$.
Donc $\cos x \geqslant \dfrac12 \Leftrightarrow x \in \left[-\dfrac{\pi}3 \,; \dfrac{\pi}3 \right]$
-
-
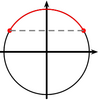
Résoudre sur $[-\pi\,; \pi]$ : $\sin x > \dfrac12$.Aide
 Solution
Solutionles réels de $[-\pi\,; \pi]$ ayant pour sinus $\dfrac12$ sont $\dfrac{\pi}6$ et $\dfrac{5\pi}6$.
Donc $\cos x > \dfrac12 \Leftrightarrow x \in \left]\dfrac{\pi}6 \,; \dfrac{5\pi}6 \right[$
-
Résoudre sur $[-\pi\,; \pi]$ : $\cos x < -\dfrac{\sqrt2}2$.Aide
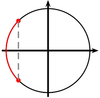
-
Résoudre sur $[-\pi\,; \pi]$ : $\sin x \leqslant -\dfrac{\sqrt3}2$.Aide
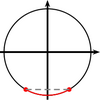 Solution
Solutionles réels de $[-\pi\,; \pi]$ ayant pour sinus $-\dfrac{\sqrt3}2$ sont $-\dfrac{2\pi}3$ et $-\dfrac{\pi}3$.
Donc $\sin x < -\dfrac{\sqrt3}2 \Leftrightarrow x \in \left[-\dfrac{2\pi}3\,; -\dfrac{\pi}3 \right]$
-
clique ici pour écrire «vrai» si la réponse à la question 2b est : $x \in \left] -\dfrac{3\pi}4 \,; \dfrac{3\pi}4 \right[$ ou «faux» dans le cas contraire.
p.230 nº 106
-
Résoudre dans $\intof{-\pi}{\pi}$ :
- $\cos x = \ffrac12$
- $\cos x = \ffrac{-\sqrt2}2$
- $\sin x = \ffrac{\sqrt3}2$
- $\sin x = -\ffrac12$
AideTravailler dans le cercle trigonométrique, puis :
- tracer la droite d'équation $x=\ffrac12$
- tracer la droite d'équation $x=\ffrac{-\sqrt2}2$
- tracer la droite d'équation $y=\ffrac{\sqrt3}2$
- tracer la droite d'équation $y=-\ffrac12$
Solution- $\cos x = \ffrac12 \iff x = -\ffrac{\pi}3 \text{ ou } x = \ffrac{\pi}3$
- $\cos x = \ffrac{-\sqrt2}2 \iff x = -\ffrac{3\pi}4 \text{ ou } x = \ffrac{3\pi}4$
- $\sin x = \ffrac{\sqrt3}2 \iff x = \ffrac{\pi}3 \text{ ou } x = \ffrac{2\pi}3$
- $\sin x = -\ffrac12 \iff x = -\ffrac{5\pi}6$ \text{ ou } x = -\ffrac{\pi}6$
-
Résoudre les équations de la question 1 dans $\intfo{0}{\pi}$, puis dans $\setR$.Solution
sur $\intfo0{2\pi}$
- $\cos x = \ffrac12 \iff x = \ffrac{\pi}3\text{ ou } x = \ffrac{5\pi}3$
- $\cos x = \ffrac{-\sqrt2}2 \iff x = \ffrac{3\pi}4\text{ ou } x = \ffrac{5\pi}4$
- $\sin x = \ffrac{\sqrt3}2 \iff x = \ffrac{\pi}3\text{ ou } x = \ffrac{2\pi}3$
- $\sin x = -\ffrac12 \iff x = \ffrac{7\pi}6\text{ ou } x = \ffrac{11\pi}6$
sur $\setR$
- $\cos x = \ffrac12 \iff x = -\ffrac{\pi}3 + 2k\pi \text{ ou } x = \ffrac{\pi}3 + 2k\pi$
- $\cos x = \ffrac{-\sqrt2}2 \iff x = -\ffrac{3\pi}4 + 2k\pi\text{ ou } x = \ffrac{3\pi}4 +2k\pi$
- $\sin x = \ffrac{\sqrt3}2 \iff x = \ffrac{\pi}3 + 2k\pi \text{ ou } x = \ffrac{2\pi}3 + 2k\pi$
- $\sin x = -\ffrac12 \iff x = -\ffrac{5\pi}6 + 2k\pi \text{ ou } x = -\ffrac{\pi}6 + 2k\pi$
p.230 nº 107
-
Résoudre dans $\intff{-\pi}{\pi}$ :
- $\cos^2 x = 1$
- $2\sin^2 x - 1 = 0$
Aide- On pose $X = \cos x$ (avec $X \in \intff{-1}1$) ; l'équation devient $X^2 = 1$ ; puis connaissant la (les) solutions $X$, on trouve les valeurs $x$.
- On pose $X = \sin x$ (avec $X \in \intff{-1}1$) ; l'équation devient $2 X^2 - 1 = 0 $ ; puis connaissant la (les) solutions $X$, on trouve les valeurs $x$.
Solution$X^2 = 1 \iff X=-1 \text{ ou } X=1$
$X = -1 \iff \cos x = -1 \iff x= -\pi \text{ ou } x=\pi$
$X = 1 \iff \cos x = 1 \iff x= 0$
donc l'équation admet trois solutions sur $\intff{-\pi}{\pi}$ : $\lbrace -\pi\,; 0 \,; \pi \rbrace$.
$2 X^2 - 1 = 0 \iff X = -\dfrac{\sqrt2}2 \text{ ou } X = \dfrac{\sqrt2}2$
$X = -\dfrac{\sqrt2}2 \iff \sin x = -\dfrac{\sqrt2}2 \iff x = -\dfrac{3\pi}4 \text{ ou } x =\dfrac{3\pi}4$
$X = \dfrac{\sqrt2}2 \iff \sin x = \dfrac{\sqrt2}2 \iff x = -\dfrac{\pi}4 \text{ ou } x =\dfrac{\pi}4$
donc l'équation admet quatre solutions sur $\intff{-\pi}{\pi}$ : $\lbrace -\dfrac{3\pi}4 \,; -\dfrac{\pi}4 \,; \dfrac{\pi}4\,; \dfrac{3\pi}4 \rbrace$.
-
Résoudre dans $\intff{0}{2\pi}$ :
\[ 2\sin^2x + 5\sin x- 3 = 0\]
Aidequand on pose $X = \sin x$, il faut $X \in \intff{-1}1$.
-
Résoudre dans $\intff{0}{2\pi}$ :
\[ -\sin^2x + 2\cos x + 2 = 0\]
Aidetravailler uniquement avec des cosinus à l'aide de la relation $\cos^2 x + \sin^2 x = 1$
clique ici pour écrire la somme du nombre de solutions trouvées aux questions 2 et 3.
p.227 nº 89
-
ConjecturesAide
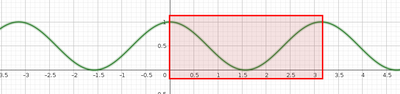
on remarque une symétrie et un motif qui se répète.
Solutionparité
La courbe semble symétrique par rapport à l'axe des ordonnées, la fonction serait paire
périodicité
la fonction semble π-périodique.
-
DémonstrationAide
fonction paire : pour tout $x \in \setR : f(-x) = f(x)$.
fonction π-périodique : pour tout $x \in \setR : f(x + \pi) = f(x)$
Solutionparité
il faut vérifier que pour tout $x \in \setR : f(-x) = f(x)$.
on sait que pour tout $x \in \setR : \cos(-x) = \cos(x)$, donc $(\cos(-x))^2 = (\cos(x))^2$ : la fonction $f$ est paire.
périodicité
il faut vérifier que pour tout $x \in \setR : f(x + \pi) = f(x)$
on sait que pour tout $x \in \setR : \cos(x + \pi) = -\cos(x)$ donc $(\cos(x + \pi))^2 = (-\cos(x))^2 = (\cos(x))^2$ : la fonction $f$ est π-périodique.
clique ici pour écrire «vrai» si les fonctions $x \mapsto \sin(x)$ et $x \mapsto (\sin(x))^2$ ont la même parité ou «faux» sinon.