Exercices : variables aléatoires

• p.358 nº 61
• p.360 nº 69
• p.361 nº 73
• p.362 nº 79
• p.362 nº 78
• p.356 nº 49

p.358 nº 61

1. Loi de proba de $X$.
   Aide

   Il y a $23$ recettes en tout, donc $p(X = 0) = \ffrac2{23}$
   Solution

   $\begin{array}{l*6c} \hline x_i & 0 & 1 & 2 & 3 & 4 & 6 \\\hline p(X = x_i) & \frac2{23} & \frac5{23} & \frac8{23} & \frac{3}{23} & \frac{4}{23} & \frac{1}{23} \\ \hline \end{array}$
2. $6$ œufs pour le clafouti
   Aide

   Il faut calculer $p(X = 6)$
3. recette impossible à faire.
   Aide

   Elle ne pourra faire de recette qui demandent plus de 2 œufs.

p.360 nº 69

1. Tableau des effectifs
   Solution

   $\begin{array}{l*3c} \hline & F & \bar{F} & \text{Total} \\\hline S & 8 & 8 & 16 \\\hline \bar{S} & 4 & 180 & 184 \\\hline \text{Total} & 12 & 188 & 200 \\ \hline \end{array}$
2. 1. Loi de probabilité de $X$.
      Aide 1

      On peut faire un tableau pour présenter le montant des réparations en fonction des défauts possibles.

      $\begin{array}{lcc} \hline & F & \bar{F} \\\hline S & 58 & \searrow 15\,\% \text{ de } 250 \\\hline \bar{S} & 45 & 0 \\\hline \end{array}$

      Aide 2

      Le bénéfice est le prix de vente diminué du coût de fabrication (et de l'éventuelle remise dûe aux défauts).
   2. Calculer $p(X \leqslant 0)$
      Solution

      $p(X \leqslant 0) = \np{0,04}$, dans 4% des cas, l'entreprise ne réalise pas de bénéfice.

p.361 nº 73

1. Loi de proba de $X$.
   Aide

   Il y a 2 cases rouges parmi les 30, donc et atteindre une case rouge rapporte 8 € ; donc $p(X= 8) = \dfrac2{30}$.
   Solution

   $\begin{array}{lcccc} \hline x_i & 8 & 5 & 0 & -a \\\hline p(X = x_i) & \frac2{30} & \frac4{30} & \frac6{30} & \frac{18}{30} \\ \hline \end{array}$
2. Espérance nulle (jeu équitable).
   Aide

   Exprimer $E(X)$ en fonction de $a$, puis résoudre une équation.
   Solution

   $E(X) = \dfrac{36 - 18a}{30}$

clique ici pour écrire la valeur $a$ qui rend le jeu équitable.

p.362 nº 79

1. Compléter tableau des fréquences.
   Aide

   parmi eux : penser à changer de référentiel !
   Solution

   $\begin{array}{lccc} \hline & \text{Vin en supplément} & \text{Pas de vin} & \text{Total} \\\hline \text{Menu express} & 42 & \color{blue}{18} & 60 \\\hline \text{Menu du jour} & \color{blue}{16} & \color{blue}{24} & \color{blue}{40} \\\hline \text{Total} & \color{blue}{58} & \color{blue}{42} & 100 \\\hline \end{array}$
2. 1. Loi de probabilité de $D$.
      Aide

      On s'aider d'un tableau donnant toutes les dépenses :

      $\begin{array}{lcc} \hline & \text{Vin en supplément} & \text{Pas de vin} \\\hline \text{Menu express} & 14 & \dots \\\hline \text{Menu du jour} & \dots & \dots \\\hline \end{array}$

      Solution

      $\begin{array}{lcccc} \hline d_i & 12 & 14 & 15 & 17 \\\hline p(D = d_i) & 0,18 & 0,42 & 0,24 & 0,16 \\\hline \end{array}$
   2. Espérance de $D$.
      Solution

      $E(D) = 0,18 \times 12 + 0,42 \times 14 + 0,24 \times 15 + 0,16 \times 17 = 14,36$

      Le restaurateur peut espérer gagner 14,36 € par client.

3. 1. Recette hebdomadaire pour 200 repas par déjeuner.
      Aide

      donc 200 × 7 repas par semaine

      Solution

      Il peut espérer : 200 × 7 × 14,36 = 20104 € par semaine.
   2. Augmentation des prix de 10% et baisse de 10% de la fréquentation.
      Aide

      Si $D'$ est la nouvelle dépense (en euros), remarquer que $D' = a D$ et utiliser la linéarité de l'espérance (ou bien refaire tous les calculs ;-)

clique ici répondre par "oui" si le restaurateur augmente son bénéfice espéré et par "non" dans le cas contraire.

p.362 nº 78

1. 1. Valeurs prises par $X$.
      Aide

      Rappel : un gain algébrique peut prendre des valeurs négatives.
      Solution

      $X$ peut prendre les valeurs -3 ; -2; 1; ou 7.
   2. Loi de probabilité de $X$.
      Aide

      Construire un arbre ?
      Solution

      

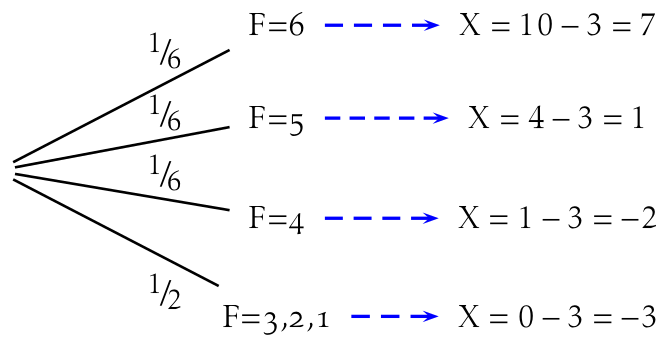
      $\begin{array}{lcccc} \hline x_i & -3 & -2 & 1 & 7 \\\hline p(X = x_i) & \frac12 & \frac16 & \frac16 & \frac16 \\\hline \end{array}$

   3. Espérance de $X$.
      Solution

      $E(X) = -\dfrac12$
   4. Bénéfice pour 150 parties.
      Aide

      Pour chaque partie, on connaît l'espérance de gain du joueur.
      Solution

      L'espérance de gain du joueur est -0,5 €, donc celui de l'organisateur est de 0,5 €.

      0,5 × 150 = 75. Le bénéfice théorique est de 75 €.

2. Mise qui rend le jeu équitable.

clique ici pour écrire pour écrire la valeur de la mise en centimes qui rend le jeu équitable.

p.356 nº 49

1. Espérance de $X$.
   Aide

   $E(X) = -3 \times 0,6 + (-2) \times 0,2 + \dots$
2. Multiplication par $2$ des valeurs de $X$.
   Aide

   La nouvelle espérance, notée $E_2$ est donc égale à : $E_2(X) = -3 {\color{red}{\times 2}} \times 0,6 + (-2) {\color{red}{\times 2}} \times 0,2 + \dots$

3. Augmmentation de 10% de valeurs de $X$.
   Aide

   Augmenter de $10\,\%$ c'est multiplier par $\left( 1 + \ffrac{10}{100} \right)$