Les exercices

Suites arithmétiques Suites géométriques

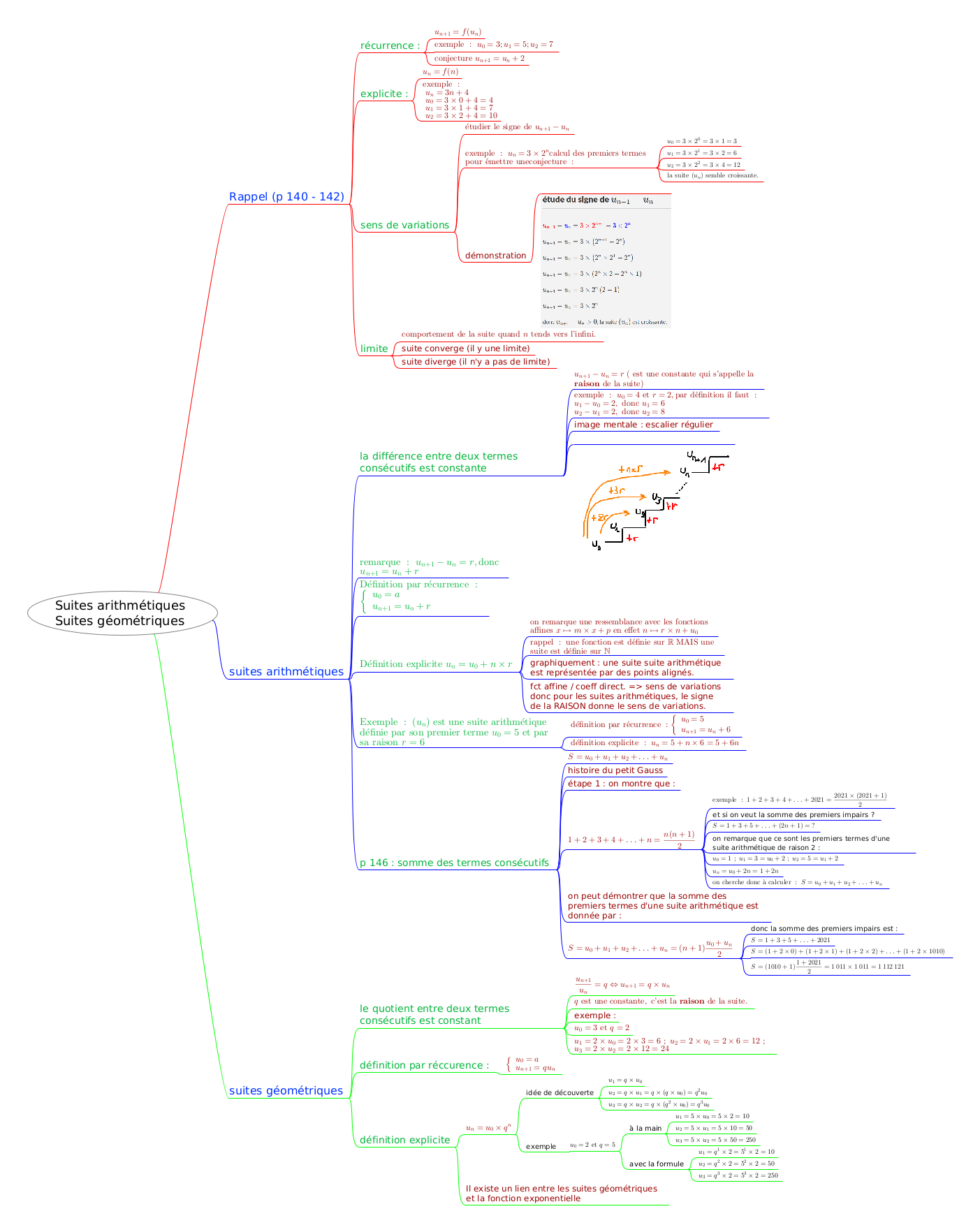
Suites arithmétiques
Suites géométriques

Rappel (p 140 - 142)

récurrence :

\( u_{n+1} = f(u_n) \)

exemple : \( u_0 = 3 ; u_1 = 5 ; u_2 = 7 \)

conjecture \( u_{n+1} = u_n + 2 \)

explicite :

\( u_n = f(n) \)

exemple : \\ \( u_n = 3 n+ 4 \\ u_0= 3 \times 0 + 4 = 4 \\ u_1= 3 \times 1 + 4 = 7 \\ u_2= 3 \times 2 + 4 = 10 \)

sens de variations

étudier le signe de \( u_{n+1}-u_n \)

exemple : \( u_n = 3 \times 2^n \)
calcul des premiers termes pour émettre une
conjecture :

\( u_0 = 3 \times 2^0 = 3 \times 1 = 3 \)

\( u_1 = 3 \times 2^1 = 3 \times 2 = 6 \)

\( u_2 = 3 \times 2^2 = 3 \times 4 = 12 \)

la suite \( (u_n) \) semble croissante.

démonstration

limite

comportement de la suite quand \( n \) tends vers l'infini.

suite converge (il y une limite)

suite diverge (il n'y a pas de limite)

suites arithmétiques

la différence entre deux termes consécutifs est constante

\( u_{n+1} -u_n = r \) ( est une constante qui s'appelle la \textbf{raison}{} de la suite)

exemple : \( u_0 = 4 \) et \( r = 2 \),
par définition il faut : \\
\( u_1 - u_0 = 2 \), donc \( u_1 = 6 \) \\
\( u_2 - u_1 = 2 \), donc \( u_2 = 8 \)

image mentale : escalier régulier

remarque : \( u_{n+1} - u_n = r \),
donc \( u_{n+1} = u_n + r \)

Définition par récurrence : \\
\( \left\lbrace \begin{array}{l}
u_0 = a \\
u_{n+1} = u_n + r
\end{array}\right. \)

Définition explicite \( u_n = u_0 + n \times r \)

on remarque une ressemblance avec les fonctions affines \( x \mapsto m \times x + p \)
~en effet \( n \mapsto r \times n + u_0 \)

rappel : une fonction est définie sur \( \mathbb{R} \) MAIS une suite est définie sur \( \mathbb{N} \)

graphiquement : une suite suite arithmétique est représentée par des points alignés.

fct affine / coeff direct. => sens de variations
donc pour les suites arithmétiques, le signe de la RAISON donne le sens de variations.

Exemple : \( (u_n) \) est une suite arithmétique définie par son premier terme \( u_0 = 5 \) et par sa raison \( r=6 \)

définition par récurrence :
\( \left\lbrace \begin{array}{l}
u_0 = 5 \\
u_{n+1} = u_n + 6
\end{array}\right. \)

définition explicite : \( u_n = 5 + n \times 6 = 5 + 6n \)

p 146 : somme des termes consécutifs

\( S = u_0 + u_1 + u_2 + \ldots + u_n \)

histoire du petit Gauss

étape 1 : on montre que :

\( 1 + 2 + 3 + 4 + \ldots + n = \dfrac{n(n+1)}{2} \)

exemple : \( 1 + 2 + 3 + 4 + \ldots + 2021 = \dfrac{2021 \times (2021 + 1)}{2} \)

et si on veut la somme des premiers impairs ?

\( S = 1 + 3 + 5 + \ldots + (2n+1) = ? \)

on remarque que ce sont les premiers termes d'une suite arithmétique de raison 2 :

\( u_0= 1 \) ; \( u_1 = 3 = u_0 + 2 \) ; \( u_2 = 5= u_1 + 2 \)

\( u_n = u_0 + 2n = 1 + 2n \)

on cherche donc à calculer : \( S = u_0 + u_1 + u_2 + \ldots + u_n \)

on peut démontrer que la somme des premiers termes d'une suite arithmétique est donnée par :

\( S = u_0 + u_1 + u_2 + \ldots + u_n = (n+1) \dfrac{u_0 + u_n}{2} \)

donc la somme des premiers impairs est :

\( S = 1 + 3 + 5 + \ldots + 2021 \)

\( S = (1 + 2\times 0) + (1 + 2 \times 1) + (1 + 2 \times 2) + \ldots + (1 + 2 \times 1010)

\)S = (1010+1) \dfrac{1 + 2021}{2} = 1\,011 \times 1\,011 = 1\,112\,121\(

suites géométriques

le quotient entre deux termes consécutifs est constant

\(\dfrac{u_{n+1}}{u_n} = q \Leftrightarrow u_{n+1} = q \times u_n\)

\(q\) est une constante, c'est la \textbf{raison}{} de la suite.

exemple :

\(u_0 = 3\) et \(q = 2\)

\(u_1= 2 \times u_0 = 2 \times 3 = 6\) ; \(u_2= 2 \times u_1 = 2 \times 6 = 12\) ; \(u_3= 2 \times u_2 = 2 \times 12 = 24\)

définition par réccurence :

\(\left\lbrace\begin{array}{l} u_0 = a \\ u_{n+1} =q u_n \end{array}\right.\)

définition explicite

\(u_n = u_0 \times q^n\)

idée de découverte

\(u_1 = q \times u_0\)

\(u_2 = q \times u_1 = q \times (q \times u_0) = q^2 u_0\)

\(u_3 = q \times u_2 = q \times (q^2 \times u_0) = q^3 u_0\)

exemple

\(u_0 =2\) et \(q=5\)

à la main

\(u_1 = 5 \times u_0 = 5 \times 2 = 10\)

\(u_2 = 5 \times u_1 = 5 \times 10 = 50\)

\(u_3 = 5 \times u_2 = 5 \times 50 = 250\)

avec la formule

\(u_1 = q^1 \times 2 = 5^1 \times 2 = 10\)

\(u_2 = q^2 \times 2 =5^2 \times 2 = 50\)

\(u_3 = q^3 \times 2 = 5^3 \times 2 =250\)

Il existe un lien entre les suites géométriques et la fonction exponentielle