- la feuille de cours .pdf
- les exercices de ce cours
- 1. Enroulement de la droite des réels sur le cercle trigonométrique
- 2. Cosinus et sinus d'un nombre réel
- 3. Fonctions sinus et cosinus
Enroulement sur le cercle
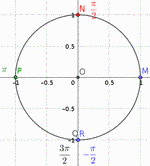
Le cercle trigonométrique
Enroulement de la droite des réels sur le cercle trigonométrique
- La vidéo d' Ivan Monka
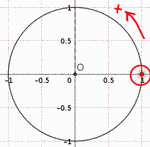
- On commence toujours à compter la distance parcourue sur le
cercle à partir du point (1;0) (en rouge sur la figure) puis on
parcours le cercle suivant le sens trigonométrique.
- un autre vidéo d' Ivan Monka
- les numérateurs étant de taille "raisonnable", on peut compter "à la main" ou bien enlever les multiples de \(2\pi\) car ils représentent un tour complet.
- le sens positif est le sens trigonométrique (sens inverse des aiguilles d'une montre).
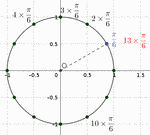 On peut compter le nombre de \(\dfrac{\pi}{6}\) ou bien remarquer que
\(\dfrac{13\pi}{6} = \dfrac{12\pi}{6} + \dfrac{\pi}{6} = 2\pi + \dfrac{\pi}{6}\) ;
le \(2\pi\) indiquant qu'on vient de parcourir un tour du cercle.
On peut compter le nombre de \(\dfrac{\pi}{6}\) ou bien remarquer que
\(\dfrac{13\pi}{6} = \dfrac{12\pi}{6} + \dfrac{\pi}{6} = 2\pi + \dfrac{\pi}{6}\) ;
le \(2\pi\) indiquant qu'on vient de parcourir un tour du cercle.
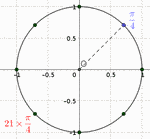 On peut compter le nombre de \(\dfrac{\pi}{4}\) (mais cela commence à faire beaucoup)
ou bien remarquer que
\(\dfrac{21\pi}{4} = \dfrac{20\pi}{4} + \dfrac{\pi}{4}
= 5\pi + \dfrac{\pi}{4}
= \color{green}{4\pi} + \color{red}{\pi} + \dfrac{\pi}{4}
\) ;
on parcourt donc 2 fois le cercle (\(4\pi\))
puis un demi-cercle (\(\pi\))
puis \(\dfrac{\pi}{4}\)
On peut compter le nombre de \(\dfrac{\pi}{4}\) (mais cela commence à faire beaucoup)
ou bien remarquer que
\(\dfrac{21\pi}{4} = \dfrac{20\pi}{4} + \dfrac{\pi}{4}
= 5\pi + \dfrac{\pi}{4}
= \color{green}{4\pi} + \color{red}{\pi} + \dfrac{\pi}{4}
\) ;
on parcourt donc 2 fois le cercle (\(4\pi\))
puis un demi-cercle (\(\pi\))
puis \(\dfrac{\pi}{4}\)
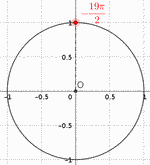 On peut compter le nombre de \(-\dfrac{\pi}{2}\) (on tourne dans le sens
inverse du sens trigonométrique = celui des aiguilles d'une montre) ;
ou bien remarquer que
\(-\dfrac{19\pi}{2} = -\dfrac{18\pi}{2} - \dfrac{\pi}{2} = -9\pi - \dfrac{\pi}{2}
= \color{green}{-8 \pi} + \color{red}{- pi} -\dfrac{\pi}{2}\) ;
on parcourt donc 4 fois le cercle (\(-8\pi\))
puis un demi-cercle (\(-\pi\))
puis \(-\dfrac{\pi}{2}\)
On peut compter le nombre de \(-\dfrac{\pi}{2}\) (on tourne dans le sens
inverse du sens trigonométrique = celui des aiguilles d'une montre) ;
ou bien remarquer que
\(-\dfrac{19\pi}{2} = -\dfrac{18\pi}{2} - \dfrac{\pi}{2} = -9\pi - \dfrac{\pi}{2}
= \color{green}{-8 \pi} + \color{red}{- pi} -\dfrac{\pi}{2}\) ;
on parcourt donc 4 fois le cercle (\(-8\pi\))
puis un demi-cercle (\(-\pi\))
puis \(-\dfrac{\pi}{2}\)
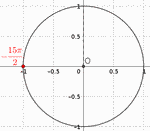 On peut compter le nombre de \(-\pi\) (on tourne dans le sens
inverse du sens trigonométrique = celui des aiguilles d'une montre) ;
ou bien remarquer que
\(-15\pi = -16\pi + \pi\) ;
on parcourt donc 8 fois le cercle (\(-16\pi\)) puis un demi-cercle (\(\pi\))
dans le sens trigonométrique.
On peut compter le nombre de \(-\pi\) (on tourne dans le sens
inverse du sens trigonométrique = celui des aiguilles d'une montre) ;
ou bien remarquer que
\(-15\pi = -16\pi + \pi\) ;
on parcourt donc 8 fois le cercle (\(-16\pi\)) puis un demi-cercle (\(\pi\))
dans le sens trigonométrique.
p 213 n° 5: placer des réels sur le cercle
- un cercle complet correspond à une longueur de \(2\pi\) ; un demi-cercle à une longueur de \(\pi\), etc.
- un triangle qui a trois égaux est équilatéral, ses angles sont égaux et valent chacun ... radian.
- \(I\) correspond à 0
- \(J\) correspond à \(\dfrac{\pi}{2}\)
- la droite \((OA)\) est la bissectrice de l'ange \(\widehat{IOJ}\) : elle le coupe en deux angles de même mesure, donc \(A\) correspond à \(\dfrac{\pi}{4}\).
\(A'\) est le symétrique de \(A\), donc pour aller de \(A\) à \(A'\) on parcourt un demi-cercle, soit une longueur de \(\pi\) ;
donc \(A'\) est associé à \(\dfrac{\pi}{4} + \pi = \dfrac{5\pi}{4}\) : mais ce réel n'appartient pas à \(]-\pi\,; \pi]\) !
on peut associer \(A'\) à \(\dfrac{\pi}{4} \color{red}{-} \pi = -\dfrac{3\pi}{4}\) en tournant dans le sens inverse.
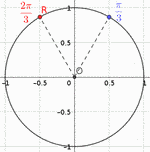
- le triangle OAB est équilatéral, donc ses angles sont égaux et valent chacun \(\dfrac{\pi}{3}\) radian. Donc \(B\) est associé à \(\dfrac{\pi}{4} + \dfrac{\pi}{3} = \dfrac{7\pi}{12}\)
- un angle de 30° correspond à un angle de \(\dfrac{\pi}{6}\) radian, donc \(C\) est associé à \(-\dfrac{\pi}{6}\).
Mesure d'un angle en radian
p 222 n° 39: angle en degré et réel associé
- \(\begin{array}{lccccc} \hline \text{angle en degré}& 0 & 30 & 45 & 60 & 90 \\\hline \text{angle en radian}& 0 & \frac{\pi}{6} & \frac{\pi}{4} & \frac{\pi}{3} & \frac{\pi}{2} \\ \hline \end{array}\)
- 150 = 180 - 30
dans \([0\,; 2\pi[\)
- \(A\) est associé à \(\dfrac{\pi}{4}\)
- \(B\) est associé à \(\pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\)
- \(C\) est associé à \(\pi + \dfrac{\pi}{2} = \dfrac{3\pi}{2}\)
- \(D\) est associé à \(2\pi - \dfrac{\pi}{3} = \dfrac{5\pi}{3}\)
dans \(]-\pi\,; \pi]\)
- \(A\) est associé à \(\dfrac{\pi}{4}\)
- \(B\) est associé à \(\pi - \dfrac{\pi}{6} = \dfrac{5\pi}{6}\)
- \(C\) est associé à \(-\dfrac{\pi}{2}\)
- \(D\) est associé à \(- \dfrac{\pi}{3}\)
Cosinus et sinus d'un nombre réel
Repérage d'un point sur le cercle trigonométrique
p 223 n° 49: signe du sinus / du cosinus
corrigé dans le livre.
p 225 n° 65: existence d'une solution
- \(\dfrac{1}{\sqrt{2}} \in [-1\,; 1]\), donc il existe au moins un réel \(x\) tel que \(\cos(x) = \dfrac{1}{\sqrt{2}}\)
- \(-\sqrt{2} \notin [-1\,; 1]\), donc il n'existe pas de réel \(x\) tel que \(\cos(x) = -\sqrt{2}\)
- \(-1 \in [-1\,; 1]\), donc il existe au moins un réel \(x\) tel que \(\cos(x) = -1\)
- \(0,99\,999 \in [-1\,; 1]\), donc il existe au moins un réel \(x\) tel que \(\cos(x) = 0,99\,999\)
- \(\dfrac{\sqrt{5}}{2} \notin [-1\,; 1]\), donc il n'existe pas de réel \(x\) tel que \(\cos(x) = \dfrac{\sqrt{5}}{2}\)
- \(2\sqrt{3} \notin [-1\,; 1]\), donc il n'existe pas de réel \(x\) tel que \(\sin(x) = 2\sqrt{3}\)
- \(\dfrac{2}{\sqrt{3}} \notin [-1\,; 1]\), donc il n'existe pas de réel \(x\) tel que \(\sin(x) = \dfrac{2}{\sqrt{3}}\)
- \(1 \in [-1\,; 1]\), donc il existe au moins un réel \(x\) tel que \(\sin(x) = 1\)
p 223 n° 68: cosinus connaissant le sinus
-
dessiner des petits cercles trigonométriques et colorier l'intervalle
concerné, puis placer approximativement le point donc le sinus est donné :
par exemple pour \(x\in \left[0\,;\dfrac{\pi}{2}\right]\) et
\(\sin(x) = \dfrac{3}{5}\)
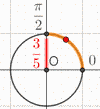
- \((\cos(x))^2 + (\sin(x))^2 = 1 \)
\(x\in \left[0\,;\dfrac{\pi}{2}\right]\) et \(\sin(x) = \dfrac{3}{5}\)
(\(\cos(x))^2 + (\sin(x))^2 = 1 \Leftrightarrow (\cos(x))^2 + \dfrac{9}{25} = 1 \Leftrightarrow (\cos(x))^2 = \dfrac{16}{25} \Leftrightarrow \cos(x) = \pm \dfrac{4}{5} \)
ATTENTION : \(x^2 = a \Leftrightarrow x = a \text{ ou } x = -a \) !!
Ici on sait (grâce à notre petit cercle trigonométrique) que \(\cos(x)>0\) ; donc \(\cos(x) = \dfrac{4}{5}\)
\(x\in \left[\dfrac{\pi}{2}\,;\pi\right]\) et
\(\sin(x) = \dfrac{3}{5}\)
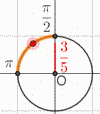
(\(\cos(x))^2 + (\sin(x))^2 = 1 \Leftrightarrow \cos(x) = \pm \dfrac{4}{5} \)
Ici on sait (grâce à notre petit cercle trigonométrique) que \(\cos(x) < 0\) ; donc \(\cos(x) = -\dfrac{4}{5}\)
\(x\in \left[\dfrac{3\pi}{2}\,;2\pi\right]\) et
\(\sin(x) = -\dfrac{2}{5}\)
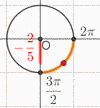
(\(\cos(x))^2 + (\sin(x))^2 = 1 \Leftrightarrow \cos(x) = \pm \dfrac{\sqrt{21}}{5} \)
Ici on sait (grâce à notre petit cercle trigonométrique) que \(\cos(x) > 0\) ; donc \(\cos(x) = \dfrac{\sqrt{21}}{5}\)
p 226 n° 80: angles associés
Utiliser les symétries du cercle : ajouter \(\pi\), c'est parcourir la moitié du cercle ; l'opposé de l'angle, c'est effectuer une symétrie axiale par rapport à l'axe des abscisses
\(a\in \left[0\,;\dfrac{\pi}{2}\right]\) et \(\cos(a) = \dfrac{3}{5}\)
(\(\cos(x))^2 + (\sin(x))^2 = 1 \Leftrightarrow \sin(x) = \pm \dfrac{4}{5} \)
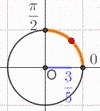 Ici on sait (grâce à notre petit cercle trigonométrique) que \(\sin(a)>0\) ;
donc \(\sin(a) = \dfrac{4}{5}\)
Ici on sait (grâce à notre petit cercle trigonométrique) que \(\sin(a)>0\) ;
donc \(\sin(a) = \dfrac{4}{5}\)
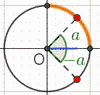 grâce au cercle trigonométrique on lit :
\(\cos(-a) = \cos(a) = \dfrac{3}{5}\)
et \(\sin(-a) = -\sin(a) = -\dfrac{4}{5}\)
grâce au cercle trigonométrique on lit :
\(\cos(-a) = \cos(a) = \dfrac{3}{5}\)
et \(\sin(-a) = -\sin(a) = -\dfrac{4}{5}\)
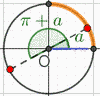 grâce au cercle trigonométrique on lit :
\(\cos(\pi + a) = -\cos(a) = -\dfrac{3}{5}\)
et \(\sin(\pi + a) = -\sin(a) = -\dfrac{4}{5}\)
grâce au cercle trigonométrique on lit :
\(\cos(\pi + a) = -\cos(a) = -\dfrac{3}{5}\)
et \(\sin(\pi + a) = -\sin(a) = -\dfrac{4}{5}\)
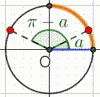 On "avance" de \(\pi\), puis on "recule" de \(a\).
Grâce au cercle trigonométrique on lit :
\(\cos(\pi - a) = -\cos(a) = -\dfrac{3}{5}\)
et \(\sin(\pi - a) = \sin(a) = \dfrac{4}{5}\)
On "avance" de \(\pi\), puis on "recule" de \(a\).
Grâce au cercle trigonométrique on lit :
\(\cos(\pi - a) = -\cos(a) = -\dfrac{3}{5}\)
et \(\sin(\pi - a) = \sin(a) = \dfrac{4}{5}\)
Ajouter \(2\pi\), c'est ajouter un tour de cercle, donc on est au même point sur le cercle : \(\cos(a + 2\pi) = \cos(a) = \dfrac{3}{5}\) et \(\sin(a + 2\pi) = \sin(a) = \dfrac{4}{5}\)
Lien avec la trigonométrie du triangle rectangle.
Valeurs remarquables des cosinus et sinus.
p 215 n° 6: sinus / cosinus
Corrigé dans le livre.
Fonctions sinus et cosinus
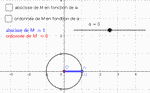
Animation GeoGebra : déplacer le curseur α
Définitions
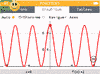
p 227 n° 83: identifier courbe
- on peut se rappeler que multiplier une fonction par un réel, dilate ou contracte la courbe de \(f\) et qu'ajouter un réel à une fonction translate "verticalement" la courbe.
- on peut aussi tracer les fonctions sur la calculatrice en se mettant en mode radian avant !
- fonction \(f\) : courbe verte
- fonction \(g\) : courbe rouge
- fonction \(h\) : courbe bleue
p 227 n° 84: identifier courbe
- fonction \(f\) : courbe verte
- fonction \(g\) : courbe bleue
- fonction \(h\) : courbe rouge
Propriétés
p 227 n° 89: étudier les propriétés d'une courbe
- une fonction \(f\) définie sur un intervalle \(D_f\) est paire si
- \(-x \in D_f \)
- pour tout \(x \in D_f : f(-x) = f(x)\)
- une fonction \(f\) définie sur un intervalle \(D_f\) est π-périodique si
- \(x + \pi \in D_f \)
- pour tout \(x \in D_f : f(x + \pi) = f(x)\)
Conjectures
le motif dans l'encadré vert est le plus petit qui permet de "dessiner la courbe par translation", sa largeur est d'environ 3 (environ \(\pi\) ?), donc une suppose que la fonction est π-périodique ; c'est à dire que \(f(x + \pi) = f(x)\)
la courbe semble symétrique par rapport à l'axe des ordonnées donc une suppose que la fonction est paire ; c'est à dire que \(f(-x) = f(x)\)
Démontrons que la fonction est périodique.
\(f(x + \pi) = (\cos(x + \pi))^2\) or \(\cos(x + \pi) = -\cos(x)\) (penser à dessiner un petit cercle trigonométrique)
donc \(f(x + \pi) = (-\cos(x))^2 = (\cos(x))^2 = f(x)\)
la fonction \(f\) est bien π-périodique.
Démontrons que la fonction est paire.
\(f(-x) = (\cos(-x))^2 \) or \(\cos(-x) = \cos(x)\) (penser à dessiner un petit cercle trigonométrique)
donc \(f(-x) = (\cos(x))^2 = f(x) \)
la fonction \(f\) est bien paire.