B.O.
Cycle 4
Notions d’inconnue, d’équation, d’indéterminée, d’identité.
Distributivité (\(k(a\pm b) = ka \pm b\) ; \((a\pm b) (c \pm d) = \dots\)), factorisation \(a^2 - b^2\), réduction.
Annulation d’un produit
Mettre un problème en équation en vue de sa résolution.
Résoudre algébriquement des équations du premier degré ou s’y ramenant (équations produits) : \(ax = b\); \(a + x = b\) ; \(x^2 = a\).
2nde
Puissances entières relatives, racines carrées, \(\sqrt{a^2} = |a|\).
Identités remarquables : \(a^2 - b^2 = (a - b)(a + b)\) ; \((a \pm b)^2 = a^2 \pm 2ab + b^2\).
Calculs sur expressions algébriques, fractionnaires, développer, factoriser, réduire.
Inégalités : somme, produit par un réel,
sens de variation fct. affine; solutions d’une équation, d’une inéquation.
Exprimer une variable en fonction des autres.
Cas du premier degré \(ax + by = c\).Comparer deux quantités (différence, quotient).
\(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\), \(\sqrt{a+b} < \sqrt{a} + \sqrt{b}\)
démonstration géométrique : \((a + b)^2 = a^2 + 2ab + b^2\)
déterminer \(n\) max tel que \(a^n < b\) (\(n\) min \(a^n > b\))
Introduction : Plimpton 322
Question : trouver des triplets Pythagoriciens.
Réponse : la tablette Plimpton 322.

Cette tablette porte le numéro 322 dans la collection Plimpton de l’université Colombia (USA). Elle est datée entre 1900 et 1600 avant Jésus Christ. Elle a été déchiffrée et analysée pour la première fois par Neugebauer et Sachs en 1945. Elle comporte quatre colonnes. La notation des nombres utilise le système babylonien en base 60.
C’est une copie d’un original perdu. Elle comporte des lacunes dues à des cassures de l’argile et des erreurs de copies…
Les Babyloniens n’utilisent que 2 chiffres :
| le clou | le chevron |
Étude de la tablette
Les colonnes sont nommées A, B, C, D à partir de la gauche.
Colonne D
Grâce à la colonne D, donner la valeur du clou et celle du chevron.
Dans la tablette, quel est le plus grand nombre écrit ?
Combien d’unités représentent les nombres suivants
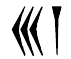 et
et  ?
Comment écrire le nombre babylonien qui vient juste après
?
Comment écrire le nombre babylonien qui vient juste après  ?
?Écrire les nombres suivants en numération babylonienne : \(185\) ; \({10805}\) et \({11100}\).
le cours du 16/01/21 : format .odt format .pdf
programmation en Python de la recherche des triplets grâce à l'application SofusPy
- Traduire les colonnes B et C, vérifier que ces nombres peuvent être les côtés d’un triangle rectangle dont le côté manquant a pour longueur un nombre entier.
Règles de calcul
p. 14
Puissances entières relatives
p 25 n°99 : calcul sur les puissances
p 26 n°102 : écriture E-03
le cours du 18/01/21 : (fichier du 16/01 complété) format .odt format .pdf
recherches et traduction de la tablette :
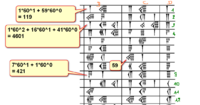
le cours du 23/01/21 : traduction de la tablette : format .odt format .pdf
Racines carrées
p 26 n°100 : calcul sur les puissances avec fractions et racines carrées
p 26 n°105 : simplifier des racines carrées
p 28 n°135 : racines carrées et puissances
25/01/21 : cours et exercices (puissances et racines carrées). format .odt format .pdf
Manipulations algébriques
p. 68
Différentes formes d’une expression algébrique
Formules de distributivité
30/01/21 : cours et exercices format .odt format .pdf
p 69 n°2 : développer et réduire
Identités remarquables
01/02/21 : cours - recherche de triplets consécutifs format .odt format .pdf
p 69 n°3 : développer id. rem et réduire
p 69 n°5 : compléter id. rem correction .odt correction .pdf
p 81 n°68 : factoriser id. rem
p 84 n°103 : démontrer à l’aide des id. rem
Techniques de factorisation
p 69 n°6 : factorisation
p 81 n°65 : factorisation
p 85 n°112 : ...
Calculs algébriques sur les quotients
p 84 n°109 : valeur et interdite et somme
Plimpton 322 :
Une méthode pour obtenir des triplets pythagoriciens (1000 ans avant Pythagore !)
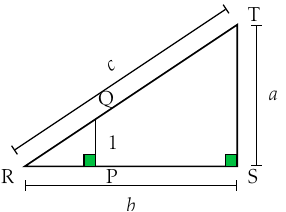
08/02/21 : une méthode pour trouver des triplets : version .odt version .pdf
Comparaison de deux quantités
p. 70
Signe et comparaison de deux nombres
p 82 n°79 : comparer sans calculatrice
Critères de comparaison de deux nombres
p 97 bilan 5 : signe de la différence
13/02/21 : correction des exercices : version .pdf et version .odt
