Découvertes

Pliages

*

Feuille A5 dans le sens paysage, placer le point \(F\) à peu près au tiers de la feuille.

Replier le bord bas de façon à passer par le point \(F\), déplier, repasser le pli en couleur. Répéter une vingtaine de fois. Les droites enveloppent une courbe.

Tracer cette courbe (elle est toujours au dessus des droites qui l’enveloppe), et l’identifier

Plier suivant la perpendiculaire au côté bas passant par \(F\), caractériser ce pli pour la courbe.

Tracer repère :

• axe des abscisses : le pli parallèle au bord bas

• axes des ordonnées : la perpendiculaire au bord bas passant par \(F\).

• coordonnées du point \(F\) : \((0\,; {0,25})\) ; le repère étant orthonormé, graduer les axes de \({0,25}\) en \({0,25}\).

• avec la précision permise par le pliage, lire les images de \({-0,5}\) ; \({0,25}\) ; \({0,75}\) et \(1\). Vérifier l’équation \(y = x^2\) pourrait être celle de la courbe.

Découpage

Fabriquer un cône, le fixer sur une feuille, faire le tour de la base avec un stylo. En déduire la nature de la section d’un cône par un plan perpendiculaire à la hauteur

placer un élastique (une ficelle) d’un point de la base à un autre, repasser le chemin sur le cône, découper.

Poser le cône le long cette découpe sur une feuille, faire le tour avec un stylo. En déduire la nature de la section d’un cône par un plan coupant la base.

Fichiers GeoGebra

Rappels : fonctions affines

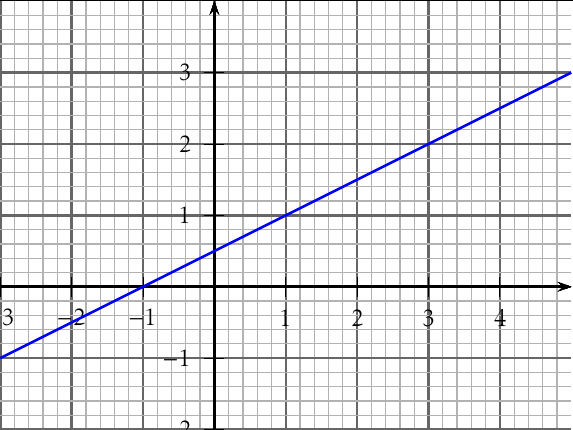
Fichier affine.ggb sur mon site.

Modifier les valeurs des curseurs \(m\) et \(p\).

Graphiquement,

• \(p\) représente …

• \(m\) représente …

Recopier et compléter le schéma expliquant comment lire les valeurs de \(m\) et \(p\) sur le graphique.

Fonction degré 2

* Fichier poly2.ggb sur mon site.

La fonction \(f\) est définie par \(f(x) = a x^2 + bx + c\)

Modifier les valeurs des curseurs \(a\), \(b\) et \(c\) puis recopier et compléter :

Graphiquement,

• on peut lire la valeur de \(c\), c’est

• on peut connaître l’orientation vers le haut ou vers le bas grâce .

• la parabole est plus ou moins dilatée (ou contractée ) en fonction .

Fichier poly2_fc.ggb sur mon site.

La fonction \(f\) est définie par sa forme canonique : \(f(x) = a (x - \alpha)^2 + \beta\)

Modifier les valeurs des curseurs \(a\), \(\alpha\) et \(\beta\) puis recopier et compléter :

Graphiquement,

• pour une valeur de \(a\) fixée, la parabole est translatée par le vecteur .

• le sommet de la parabole a pour coordonnées .

Variations et courbe représentative

Sens de variations

p 52 n°31 : SANS calculatrice - reconnaître courbe

Tableau de variations à partir de la forme canonique.

Courbe représentative

p 43 n°1 : sommet - axe de symétrie

p 43 n°4 : sommet - axe de symétrie + équation

p 57 n°77 : retrouver équation

p 115 n°60 : modélisation - forme canonique

polynôme second degré / parabole

graphique : orientation en fonction de \(a\), axe de symétrie, coordonnées du sommet.

Position par rapport aux axes du repère

p 52 n°35 : forme canonique + schématiser parabole

p 54 n°53 : modéliser

Intersection avec ordonnées \((0\,; c)\)

Intersection avec l’axe des abscisses : au maximum deux points.

p 53 n°54 : https://www.reims.fr/economie-emplois/les-marches/les-halles-du-boulingrin-8381.html donne une erreur 404 quand on clique sur le lien Laissez vous conter les Halles du Boulingrin… Essayer de trouver ce document !

Signe d’un polynôme du second degré

p 58 n°83 : signe poly degré 2

p 58 n°87 : inéquation

p 53 n°45 : modéliser, étude de signe

p 58 n°98 : lecture graphique / calcul

p 59 n°109 : lecture graphique / calcul

Tableau récapitulatif en fonction des valeurs de \(a\) et de \(\Delta\).