B.O.

• Unique fonction dérivable vérifiant \(f' = f\) et \(f(0) = 1\). (existence et unicité admises.) Notation \(\exp(x)\), \({\text{e}}^x\), propriétés algébriques. Signe, variation, courbe.

• La suite \(\left({\text{e}}^{na}\right)\) est géométrique.

• Transformer une expression.

• Modéliser une situation.

• Construction par la méthode d’Euler, \(\lim_{n \to +\infty} \left( \left(1 + \frac{1}{n} \right)^n \right) = {\text{e}}\).

Introduction

Ce cours complète celui du livre (Déclic, page 178 et suivantes) ;

• vous entendez régulièrement parler de croissance exponentielle de la maladie…

• vous connaissez les règles de calculs avec les puissances relatives.

• vous connaissez les formules de dérivation des fonctions usuelles.

• vous connaissez les règles de dérivation plus compliquées :

  Produit :

  la dérivée de \(u(x) \times v(x)\) est \(u'(x) \times v(x) + u(x) \times v'(x)\) ;

  Quotient :

  la dérivée de \({\dfrac{u(x)}{v(x)}}\) est \({\dfrac{u'(x) v(x) - u(x) v'(x)}{(v(x))^2}}\)

  Composition

  par une fonction affine : la dérivée de \(f(x) = u(mx + p)\) est \(f'(x) = m \times u'(mx + p)\).

• vous connaissez les suites géométriques : expression (explicite, par récurrence), représentation graphique, sens de variation.

Question théorique

Une équation dont l’inconnue est une fonction

Remarque : si \(f\) est une fonction et \(f'\) sa fonction dérivée, on remarque que presque toujours : \(f'(x) \neq f(x)\). En effet :

• \(f(x) = 0\), a pour dérivée \(f'(x) = \dots\)

• \(f(x) = k\) avec \(k\) un réel non nul, a pour dérivée \(f'(x) = \dots\)

• \(f(x) = x^2\) a pour dérivée \(f'(x) = \dots\)

• \(f(x) = {\dfrac{3}{x}}\) a pour dérivée \(f'(x) = \dots\)

• \(f(x) = (3x + 2) \times \sqrt{x}\) a pour dérivée \(f'(x) = \dots\)

• \(f(x) = {\dfrac{3x + 2}{x- 4}}\) a pour dérivée \(f'(x) = \dots\)

Question : existe-t-il une fonction \(f\), définie sur \({\mathbb{R}}\), autre que qui soit égale à sa dérivée, c’est à dire telle que pour tout réel \(x\) on ait \(f'(x) = f(x)\) ?

Dans cette équation l’inconnue est la fonction \(f\).

26/04/21 : déconnexion de l'ENT toutes les 5 minutes... Introduction du cours : prise de notes

30/04/21 : youpi : cela fonctionne ! cours "un peu" difficile... suite de la prise de notes (~530 Kio) et la feuille tableur (LibO) pour compléter les tableaux de valeurs.

Calcul d’images

Supposons qu’il existe une fonction \(f\) définie sur \({\mathbb{R}}\) telle que qui soit égale à sa dérivée. C’est à dire telle que : \(f(x) = f'(x)\) et que \(f(0) = 1\) (ce n’est donc pas la fonction nulle !).

L’idée est de calculer une valeur approchée des images.

Par définition : pour tout réel \(a\), \(f'(a) = \) Ce qui signifie que si \(h\) est très petit : \(f'(a) \approx {\dfrac{f(a + h) - f(a)}{h}}\)

On va simplifier en admettant l’égalité pour \(h\) très petit et strictement positif, c’est à dire on va écrire : \(f'(a) \fbox{$=$} {\dfrac{f(a + h) - f(a)}{h}}\)

1. En admettant l’égalité \(f'(a) = {\dfrac{f(a + h) - f(a)}{h}}\), exprimer \(f(a + h)\) en fonction de \(f'(a)\) et \(f(a)\).

2. Or la fonction \(f\) est telle que pour tout \(x\) réel, \(f'(x) = f(x)\). En déduire une expression de \(f(a + h)\) en fonction de \(f(a)\).

3. D’après cette relation, pour \(h > 0\) et \(f(a) > 0\), on a : \(f(a + h)\) \( f(a)\) ; donc la fonction \(f\) est sur \([0\,; +\infty[\), car on a posé \(f(0) = 1\), donc \(f(0) > 0\).

4. Compléter les tableaux suivants (on devra s’aider d’un tableur).

   pour \(h = 1\) (pour tester les formules, car \(1\) n’est pas très petit )

   \(\begin{array}{l*{10}{c}} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\\hline f(x) & 1 & 2 & 4 & {} & {} & {} & {} & {} & {} & {} \\ \hline\end{array} \)

   pour \(h = {0,1}\) \(h\) est petit , il faut lignes de tableur pour pouvoir remplir le deuxième tableau.

   \(\begin{array}{l*{10}{c}} \hline x & 0 & 0,1 & 0,2 & 0,3 & & & & & & 0,9 \\ \hline f(x) & 1 & 1,1 & 1,21 & & & & & & & \\ \hline\end{array} \)

   \(\begin{array}{l*{10}{c}} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline f(x) & 1 & 2,594 & 6,727 & & & & & & & \\ \hline\end{array} \)

   pour \(h = {0,01}\) \(h\) est très petit , il faut lignes de tableur pour pouvoir remplir le deuxième tableau.

   \(\begin{array}{l*{10}{c}} \hline x & 0 & 0,01 & 0,02 & 0,03 & & & & & & 0,09 \\ \hline f(x) & 1 & 1,01 & 1,02 & & & & & & & \\ \hline\end{array} \)

   \(\begin{array}{l*{10}{c}} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline f(x) & 1 & 2,7048 & 7,316 & & & & & & & \\ \hline\end{array} \)

Propriété

Rappel : \(f\) est dérivable et pour \(x\) réel, \(f'(x) = f(x)\) et \(f(0) = 1\).

Soit la fonction \(h\) définie sur \({\mathbb{R}}\) par \(h(x) = f(x) \times f(-x)\).

1. Calculer \(h(0)\).

2. Soit \(v\) la fonction définie sur \({\mathbb{R}}\) par \(v(x) = f(-x)\), en déduire \(v'(x)\) en fonction de \(f(x)\).

3. Calculer la dérivée de \(h\).

4. En déduire l’expression de \(h\).

Ce qui permet de conclure : pour tout \(x \in {\mathbb{R}}\) :

1. \(f(x) \neq 0\) ;

2. \(f(-x) = {\dfrac{1}{f(x)}}\) : on pourra facilement compléter les tableaux de valeurs pour les valeurs de \(x\) négatives.

3. donc \(f(x) > 0\)

Bilan

il existe une fonction définie sur \({\mathbb{R}}\) telle que :

1. pour tout réel \(x\), \(f'(x) = f(x)\)

2. \(f(0) = 1\)

pour tout \(x \in {\mathbb{R}}\) :

1. \(f(x) > 0\),

2. \(f'(x) > 0\), c’est à dire \(f\) est strictement croissante sur \({\mathbb{R}}\)

3. \(f(-x) = {\dfrac{1}{f(x)}}\)

La fonction exponentielle

p. 180

Définition

On admet l’existence de cette fonction. Elle se nomme la fonction exponentielle et se note \(\exp\).

Propriété

\(\exp(x) \times \exp(-x) = 1\) (donc \(\exp(0) \neq 0\)).

Propriétés algébriques

\(\exp(x + y) = \exp(x) \times \exp(y)\).

p 181 n°2 ; aide : \(2 = 1 + 1\); \(3 = 2 + 1\) et propriété du cours.

Notation \({\text{e}}\)

Culture : C’est à Euler qu’on doit la notation \({\text{e}}\) pour l’exponentielle. Voir l’Abécédaire des mathématiciens (pages de couverture du livre). Vous connaissez les règles de calcul à l’aides des puissances entières relatives.

Attention : les puissances non entières donnent une écriture qui facilite les calculs, mais elles ne représentent pas un nombre de multiplications !

\(x^4 = \underbrace{x \times x \times x \times x}_{4\text{ facteurs }}\)

\(2^{-3} = \left(2^{-1}\right)^3 = \left({\dfrac{1}{2}}\right)^3 = \underbrace{{\dfrac{1}{2}} \times {\dfrac{1}{2}} \times {\dfrac{1}{2}}}_{3 \text{ facteurs}}\)

\(3^{\frac{1}{2}} = \underbrace{3 \times ??}_{?? \text{ facteurs}}\)

1. Donner le résultat sous forme d’une puissance ou d’un entier inférieur à \(10\).

   1. \(2^3 \times 2^5 = \)

   2. \(10^5 \times 10^{-5} = \)

   3. \((2^3)^4 = \)

   4. \({\dfrac{8^9}{8^8}} = \)

   5. \({\dfrac{3^{10}}{3^6}} = \)

   6. \({\dfrac{4^2}{4^8}} = \)

Cas particuliers : si \(x \neq 0\), alors \(x^0 = \dots\) et pour tout \(x \in {\mathbb{R}}\) : \(x^1 = \dots\) De façon générale pour \(n\) et \(p\) entiers relatifs : \((a^n)^p = \) Certains mathématiciens ont remarqué (comme vous) que :

pour \(x \geqslant 0\) : \(\left( \sqrt{x} \right)^2 = x\)

l’idée leur est venue d’écrire \(\sqrt{x}\) comme une puissance : \(x^p\) ; on a donc

\(\left( \sqrt{x} \right)^2 = \left( x^p \right)^2 = x^{{\color{red}{\fbox{...}}}}\)

et \(\left( \sqrt{x} \right)^2 = x = x^{{\color{blue}{\fbox{...}}}}\)

donc il faut \({\color{red}{\fbox{...}}}={\color{blue}{\fbox{...}}}\) c’est à dire \(p = \dots\)

Les puissances non entières sont nées ! (mais il reste à vérifier quelques petites choses pour que ce soit mathématiquement utilisable…)

Observez les formules écrites à l’aide de la notation puissances et comparez à celles de la page 180.

Il est généralement plus naturel de travailler avec la notation puissance qu’avec l’expression de la fonction \(\exp\). C’est que nous ferons dans la suite de ce chapitre.

p 191 n°42 : développer expo

p 191 n°43 : développer expo

07/05/21 : cours et exercices p 181 n° 2 et p 191 n° 24 sur cette page.

10/05/21 : exercice p 191 n° 43

p 191 n°45 : développer expo

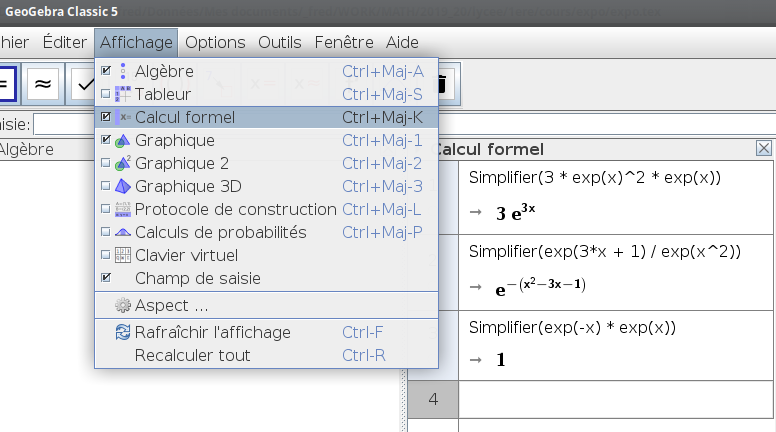
Pour vérifier vos calcul : le logiciel de calcul formel libre et gratuit Xcas. Il est un peu austère…

Donc vous pourrez utiliser sa version en ligne

ou bien GeoGebra avec la fenêtre calcul formel qui reprend une grande partie des fonctions de Xcas (mais pas linéariser…)

Lien avec les suites géométriques

Supposons que le nombre de personnes infectées par une maladie triple toutes les semaines.

Un modèle possible :

• \(u_0\) est le nombre de personnes infectées la semaine \(0\). Posons \(u_0 = 20\).

• chaque semaine le nombre de personnes nouvellement infectées triple, donc début de la première semaine, il y a \(u_1 = 60\) personnes nouvellement infectées ; puis en début de deuxième semaine : \(u_2 = 180\) …

1. Calculer les valeurs exactes de \(u_3\) ; \(u_4\) et \(u_5\).

2. Déterminer la nature de la suite \((u_n)\), préciser son premier terme et sa raison. En déduire l’expression explicite de \((u_n)\).

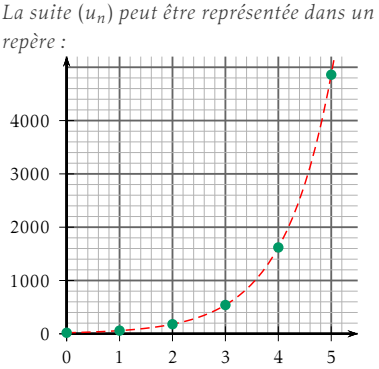
3. Déterminer le sens de variations de \((u_n)\) à partir de son expression et conjecturer sa limite quand \(n\) tend vers \(+\infty\).

Pour compléter la modélisation, il faudrait pouvoir connaître le nombre de personnes nouvellement infectées chaque jour à partir de ces données : on aimerait pouvoir connaître l’expression de la fonction dessinée en pointillés rouge et calculer les valeurs entre \(u_3\) et \(u_4\) par exemple.

Question : peut-on calculer \(u_{{3,5}}\) ?

• réponse 1 : non, car les suites sont des fonctions définies sur des entiers ;

• réponse 2 : oui, si on définit ce que sont des puissances non entières ! et donc travailler avec des fonctions au lieu de travailler avec des suites.

1. Tabuler les premières valeurs de la suite \((u_n)\).

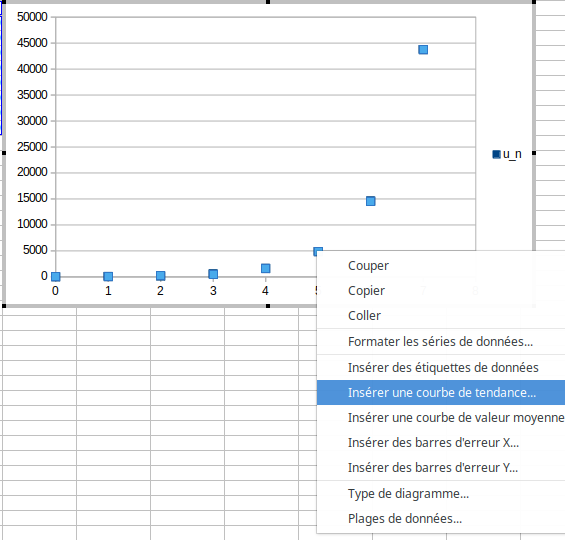
2. Construire, dans le tableur, le nuage de points associé à cette suite.

3. Déterminer une équation de la courbe de tendance exponentielle à l’aide du menu contextuel (obtenu à l’aide d’un clic-droit sur un des points du graphique).

   

p 192 n°54 : associer une fonction expo. à une suite géom.

10/05/21 : travail sur les suites. version LibO version .pdf

Étude de la fonction exponentielle

Signe et sens de variations

p 193 n°68 : signe de l’expo.

p 193 n°69 : signe de l’expo ; dans Xcas resoudre((x - 3) * exp(x) > 0, x) donne l’ensemble des solutions de l’inéquation \((x - 3) * exp(x) > 0\) en précisant que la variable est \(x\).

p 194 n°88 (corrigé dans le livre) ; dans Xcas resoudre(4*exp(-x) + 7*x*exp(-x), x), donne la liste des solution de l’équation \(4*exp(-x) + 7*x*exp(-x) = 0\) sachant que la variable est \(x\). Écrire tous les signes d’opération !

p 194 n°89 : équation quotient

p 194 n°91 : équation et changement de variable

p 196 n°100 : comparaison de deux exponentielles

p 197 n°110 : reconnaître graphique. Aide : faire l’exercice sans calculatrice, puis vérifier à l’aide de la calculatrice / d’un logiciel.

Quelle transformation géométrique permet de construire la courbe représentative de la fonction \(g\) définie sur \({\mathbb{R}}\) par \(g(x) = {\text{e}}^{-x}\) à partir de celle de \(f\) définie sur \({\mathbb{R}}\) par \(f(x) = {\text{e}}^x\) ?

p 193 n°78. Aide : tracer la fonction et vérifier que les variations correspondent au signe de la dérivée. Dans GeoGebra vérifier la dérivée en définissant \(f\), puis en tapant \(f'(x)\) en ligne de saisie.

p 198 n°117 : étude de fonction