B.O.
Vecteurs
Cycle 4
Comprendre l’effet d’une translation, d’une homothétie.
Frises, pavages
2nde
Manipuler les vecteurs du plan.
Vecteur : notation, translation, direction, sens et norme ; égalité, vecteur nul ; somme, relation de Chasles.
Base orthonormée. Coordonnées d’un vecteur, norme : \({\|{\overrightarrow{AB}}\|} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}\).Produit d’un vecteur par un nombre réel. Colinéarité,
déterminant : \(\det(\vec{u}\,; \vec{v}) = xy' - x'y\),alignement, parallélisme.
Construire géométriquement la somme de deux vecteurs.
Coordonnées du milieu d’un segment.
Géométrie
Cycle 4
Parallélogramme.
Mener des raisonnements et s’initier à la démonstration en utilisant les propriétés des figures, des configurations et des transformations.
Hauteur / médiatrices concourantes
2nde
Résoudre des problèmes de géométrie.
Introduction
À la recherche du centre de la France !Notion de vecteur
p. 130
Translation et vecteurs
Rappels :
Forces en Phy-Chi.
Translations au collège : fiche les Cavaliers d’Escher.
les diagonales d’un parallélogramme se coupent en leur milieu ; en déduire une construction sans les quadrillage.
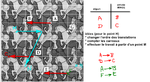
Si \(D\) image de \(C\) par translation de vecteur \({\overrightarrow{AB}}\) : un visuel pour retenir la construction : \(\begin{array}{l@{\rightarrow}l} A & B \\ C & D \end{array}\) (on voit le parallélogramme) donc \(m[AD]=m[BC]\)
Définition : \(t : M \mapsto M'\) et \(t : N \mapsto N'\) \({\Leftrightarrow}MNN'M'\) parallélogramme.
Définition : \(t : M \mapsto M'\) est la translation de vecteur \({\overrightarrow{MM'}}\)
un vecteur se caractérise par :
sa direction (inclinaison par rapport à l’horizontale)
son sens (de \(A\) vers \(B\))
sa norme (distance \(AB\)) notée \(\|{\overrightarrow{AB}}\|\)
Remarque : Si les points \(A\) et \(B\) sont confondus, alors l’image d’un point \(M\) sera lui même. Le vecteur \({\overrightarrow{AA}}\) est le vecteur nul ; on le note \({\overrightarrow{0}}\)
Intro : feuille cavaliers
01/03/21
p 142 n°38 : translation
p 142 n°47 (q. 1, 2, 3) : construction avec quadrillage
Égalité de deux vecteurs
Définition : \({\overrightarrow{AB}} = {\overrightarrow{CD}} {\Leftrightarrow}AB\color{red}{D}C \) est un parallélogramme.
\({\overrightarrow{AB}} = {\overrightarrow{CD}} {\Leftrightarrow}m[AC] = m[AB] \)
| \(N\) est l’image de \(M\) par la translation de vecteur \({\overrightarrow{AB}}\) |
| \(ABNM\) est un parallélogramme |
| \([AN]\) et \([BM]\) ont le même milieu |
p 142 n°49 : égalité / préciser : l'image de \(I\) est \(J\)
p. 146 n°89 (sauf q5) : caractéristiques des vecteurs
p. 146 n°93 : translation, parallélogramme
06/03/21 : correction feuille vecteur :
explications et
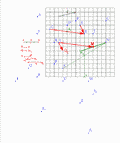 correction p. 142 n° 49 version LibreOffice
version .pdf
correction p. 142 n° 49 version LibreOffice
version .pdf
08/03/21 : exercices faits en classe

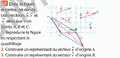
 p. 146 n° 93 (.pdf)
LibO
p. 146 n° 93 (.pdf)
LibO
Configurations usuelles du plan
p. 104
Quadrilatères particuliers
08/03/21 -> 13/30 : la feuille "quadrilatères" complétée.
Un jeu pour travailler avec les propriétés des parallélogrammes : parallelotris
p 114 n°57 : aires
Cercles et angles
Angle au centre - caractérisation du triangle rectangle
Tangente à un cercle
correction p 114 n° 57 version LibreOffice
version .pdf
début de l'exercice p 147 n° 96

Somme de deux vecteurs
p. 132
Définition et relation de Chasles
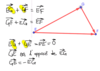
p 147 n°96 : somme et quadrillage
p 147 n°98 : somme et parallélogramme
Opposé d’un vecteur
Correction p 147 n° 96 : deux séances :
16/03/21 :
 et 20/03/21
et 20/03/21

Droites remarquables d’un triangle
p. 106
Médiatrices et autres
Définitions déjà rappelées : DM09 (aire du triangle équilatéral)
Nouveauté : points de concours.
22/03/21 : recherche des points de concours version LibO version .pdf
Projeté orthogonal d’un point sur une droite
Produit d’un vecteur par un réel
p. 132
Centre de la France.
Feuille Centre de la France
Définition et propriété
norme / sens
distributivité
Vecteurs colinéaires
29/03/21 : complément du cours
version LibO
version .pdf
et exercices
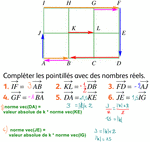
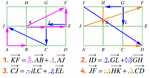 p 148 n° 122
version LibO
version .pdf
p 148 n° 122
version LibO
version .pdf
30/03/21 : exercice p. 149 n° 25